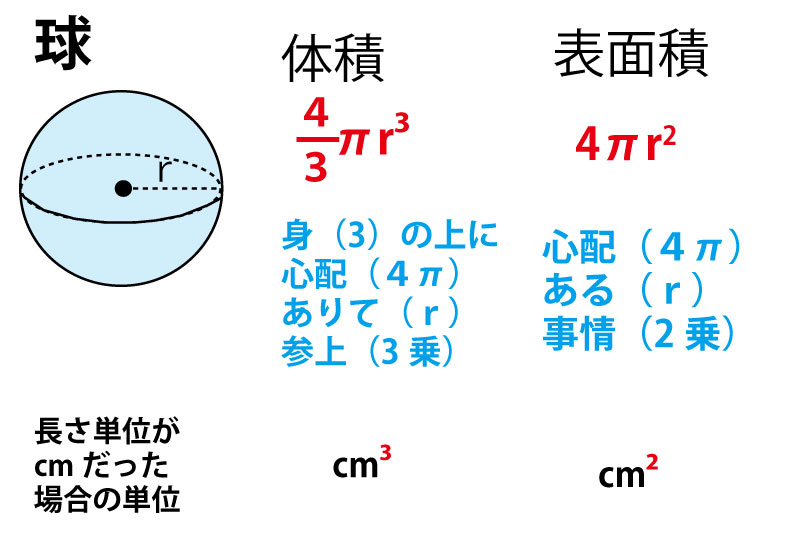
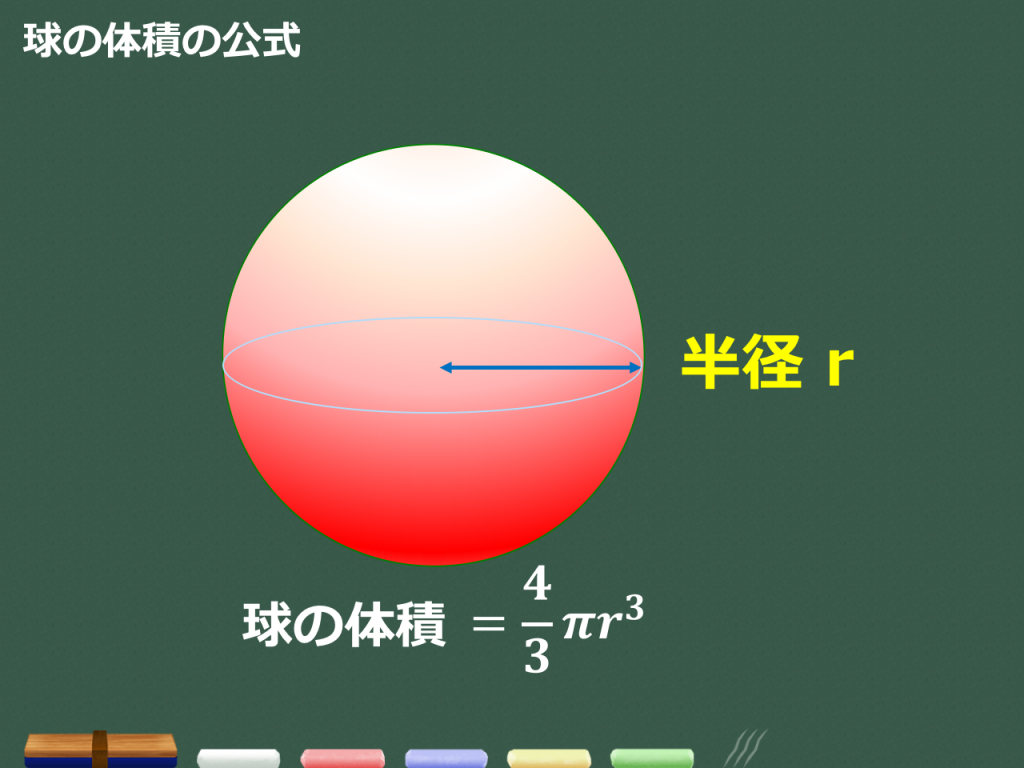
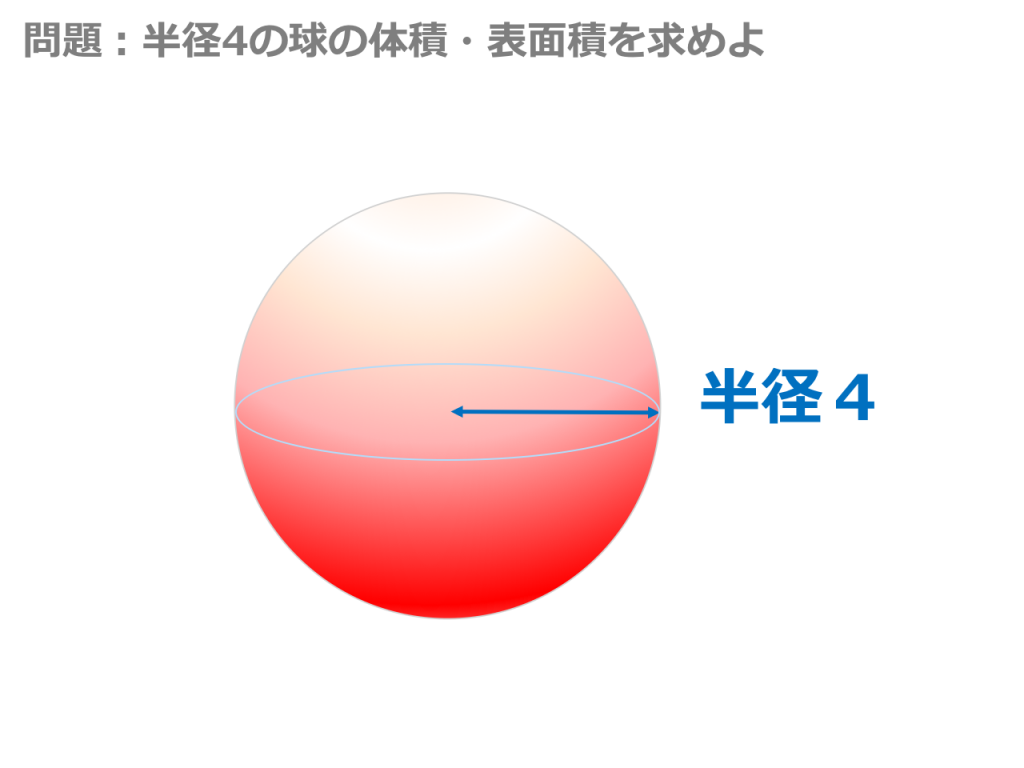
· 体積の単位には\(cm^3\)、\(m^3\)というように3乗がついているよね。 だから、公式にも\(\displaystyle \frac{4}{3}\pi r^3\)というように3乗がある。 面積の単位には\(cm^2\)、\(m^2\)というように2乗がついているよね。0118 · ぐー477" ④ 球の体積 半径が7の球の体積をしとすると, リーまァが ー 考え方と解き方 面積と体積を求める公式にあてはめて 面積 4ァ x6=144z(cmう) *積 芋zx6'=2z(om 3 國 表面積 144zcm 体積 2rem 球の表面積はその球がちょ うと人 る円柱の側面積に等しい< 球の体積は · 球の体積の公式をつかいましょう!球の体積の公式は、4πr 3 / 3でしたね。 4πr 3 / 3 にr=3を代入します。 4π×3 3 / 3 = 36π・・・(答) となります。簡単ですよね? 球の体積の公式は必ず覚えましょう! 球の表面積に関する問題

球の体積と表面積の公式と覚え方を一目でわかるように図を用いて解説します 練習問題付き 高校生向け受験応援メディア 受験のミカタ
球体 の 体積 公式
球体 の 体積 公式-球の体積と表面積 半径 r r の球の体積と表面積を求める公式は以下のようになります。 球の体積= 4 3 πr3 球 の 体 積 = 4 3 π r 3 球の表面積=4πr2 球 の 表 面 積 = 4 π r 2 「なぜこの公式が成立するのか」については中学生の知識の範囲外です。 証明に球の体積を求める公式は、次の通りです。 V = 4 3πr3 V = 4 3 π r 3 ここで、V は球の体積、r は球の半径、π は円周率を表します。




中1 数学 中1 84 球について Youtube
球の体積の公式から、表面積Sは、 (4/3) π r 3 = (1/3)・S・r より、S = 4 π r 2 以上から、 (球の表面積) = 4 π r 2 という公式が作られる。 球の体積、表面積については、いろいろな覚え方があるが、次は、有名でしょう。 · 半球の表面積 S =球の表面積の半分+半球の切り口である直径4cm(半径2cm)の円の面積であることから S = 4π × 22 × 1 2 + 22π = 8π + 4π = 12π 答え 12π cm² ~立体の体積・表面積を求める公式まとめ~ 立方体・直方体の体積の求め方 円柱の体積の求め四面体の体積 正四面体の体積 正四面体の辺の長さ 正三角柱の体積 正三角柱の高さ 正四角柱の体積 正四角柱の高さ 正六角柱の体積 正六角柱の高さ 正四角錐の体積(底辺と高さから) 正四角錐の体積(底辺と側辺から) 正四角錐台の体積 四角錐台の体積
1007 · 結果は、公式通りになったので公式を覚えておけば良いわけですが考え方は非常に重要です。 球の体積 \(x^2y^2z^2\leq R^2\) · 球の体積の求め方には公式があるんだ。 球の半径をrとすると、体積の求め方は、 $$\frac{4}{3}πr^3$$ になるよ。 つまり、 3分の4 × 円周率 × 半径 × 半径 × 半径 ってことだね。 この公式でどんなボールの体積も計算できちゃうんだ。1230 · 公式の覚え方 中学校では次のような公式を習うかと思います。 円の半径を r r 、同じく球の半径を r r とすると、 円の面積は A = πr2 A = π r 2 円周は ℓ = 2πr ℓ = 2 π r 球の体積は V = 4 3 πr3 V = 4 3 π r 3 球の表面積は S = 4πr2 S = 4 π r 2 この式を見比べてい
C言語で球の表面積と体積を求めるためのサンプルプログラム 今回は、C言語で球の半径を基に表面積と体積を求めるためのサンプルプログラムを作成したので、そのコードを紹介したいと思います! まず、コードは、下記のようになります。 #include球の体積 \(\left ( \displaystyle \frac {\pi}{6} \right ) D^3\) 球の質量 \(\left ( \displaystyle \frac {\pi}{6} \right ) D^3 \rho\) 球の体積基準比表面積(単位体積当たりの表面積) \(\displaystyle いちいち半径の公式から換算するのは能率が悪い。0114 · 球体の表面積=円柱の側面積= 方法③:球体を細かく切る 指針(考え方) 球体を切って細かくする→表面積を考える 細かく切る 球体の表面に薄いマクがはってあることをイメージする マクの面積=球の表面積 球体を図のように切る. これを6回




球の表面積の求め方 中学生の子に公式の覚え方のコツを紹介 中学や高校の数学の計算問題



U9j580gf8iba369ji2w Xyz P 296
それぞれの面積はこのように計算できます。 立方体の体積: 4× 4×4=64(cm3) 4 × 4 × 4 = 64 ( c m 3) 直方体の体積: 3× 4×5=60(cm3) 3 × 4 × 5 = 60 ( c m 3) つづいて、立方体・直方体がこれらの公式で求められる理由について説明していきます。球の表面積を 積分 = 球の体積 逆に、 円の面積を 微分 = 円周 球の体積を 微分 = 球の表面積 この関係が理解できたら、 公式丸暗記からは解放されて楽になりますね! 「積分」は、 無限に細く切った線を 足し合わせて面をつくる · なお, r 1 = 0 r_1=0 r 1 = 0 または r 2 = 0 r_2=0 r 2 = 0 とすることで球欠の体積公式: V = 1 6 π h (3 r 2 h 2) V=\dfrac{1}{6}\pi h(3r^2h^2) V = 6 1 πh (3 r 2 h 2) が得られます。




中学数学 球の表面積の求め方の公式を1発で覚える方法 Qikeru 学びを楽しくわかりやすく




球の体積公式の微分が表面積になっている理由 Youtube
の共通部分 の体積 を求めよ. 次 314 曲面積 上 3 多重積分 前 312 演習問題 ~ 多重積分の積分変数の変換 平成21年12月2日 · 半径rの球の体積を求める公式は、次のようになります。 πは円周率(=)です。 球の体積は、半径rの3乗に比例していくということですね!0810 · 球体体积计算公式为:v=(4/3)πr³ 球体表面积计算公式为:s=4πr² π表示圆周率;r表示球体的半径。 球体的定义: 定义:一个半圆绕直径所在直线旋转一周所成的空间几何体叫做球体,如图所示的图形为球体。




球の表面積 体積 中学数学から大学の数学まで広く眺める 身勝手な主張




ボード 数学 のピン
球の体積と表面積 東京大学大学院数理科学研究科・教授 古田幹雄 1 円の面積と円周の長さ 半径rの円の面積はˇr2 です。 グラフv = ˇu2 のu = rにおける接線の傾きを求めてみま す。すると、答えは2ˇrとなります。これは半径rの円周の長さです。つまり、円の面積 · 球の体積と表面積の公式: 半径 r r r の球の表面積は S = 4 π r 2 , S=4\pi r^2,\ S = 4 π r 2 , 球の体積は V = 4 3 π r 3 V=\dfrac{4}{3}\pi r^3 V = 3 4 π r 3 である。角柱と角錐の体積を求める公式 角柱と角錐の体積を求めるための公式があります。 角柱の体積=底面積×高さ 角錐の体積=底面積×高さ×1/3 これは円柱や円錐のときも同じで、円柱の体積は、「底面の円の面積×高さ」、円錐の体積は、「底面の円の面積×高




中1 数学 中1 84 球について Youtube
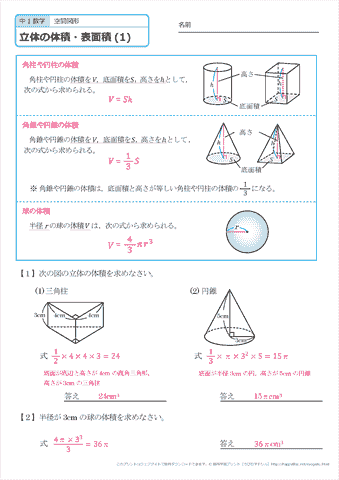



中学1年生 数学 空間図形 立体の体積と表面積 練習プリント 無料ダウンロード 印刷 ちびむすドリル 中学生
· (円柱の体積)=(底面の円の面積)×(高さ)=πr 2 ×h= πr 2 h 円柱の体積を求めるには、与えられた半径や高さをこの公式に代入すればよいのです。上の基本問題をこの公式を使って求める (1) r=5、h=10 だから、V=π ×5 2 ×10=250π cm 3 · 球体の体積を教えて下さい。 たとえば、直径2cmの球体と、直径3cmの球体、4cmの球体・・・直径が1cm違うと、どのくらい体積が違うのか、知りたいです。出来ればmlとかccとかの単位で・・・よろしくお願いします 直径が分かっているのですから、それから半径を求め、後は球の体積の公式に代入08 · 球の表面積の公式を使えば、半球の側面積(もとの球面の部分)は、 1 2 ⋅4πR2 = 2πR2 1 2 ⋅ 4 π R 2 = 2 π R 2




Excel エクセルで球の体積と表面積を計算する方法 モッカイ



球の体積の求め方とその証明 高等学校で学ぶ積分の知識が必要
『球と円柱について』(ギリシア語 Περὶ σφαίρας καὶ κυλίνδρου )は、紀元前225年ごろアルキメデスにより発表された2巻からなる著作 。 最も注目すべきは、球面の表面積や球体の体積、円柱のそれにあたる値を見つけ出す方法が詳しく書かれていることであり、アルキメデスはこれ楕円体の体積 体積 V = 4π a b c /3 楕円体の表面積 (楕円面の表面積) a ≧ b ≧ c ならば、表面積は楕円積分を用いて次式で与えられる。 · 円錐の体積の求め方の公式 は、 底面積×高さ×1/3




球の表面積と体積の公式 数学fun




楕円の面積と楕円体の体積の求め方 宇宙に入ったカマキリ
V = 体積 (角錐台) S1 = 角錐底面積 S2 = 角錐上面積 球体 V = 体積 A = 球体の表面積 r = 球体半径 楕円体 楕円体の体積 → 楕円体 楕円体の表面積 台形 A = 面積 A = 面積 ヘロンの公式 A = 面積 = bh/2 又は ヘロンの公式 jin体積 = 底面積 × 高さ




球の体積と表面積 Jsciencer




中1数学 球 練習編 映像授業のtry It トライイット
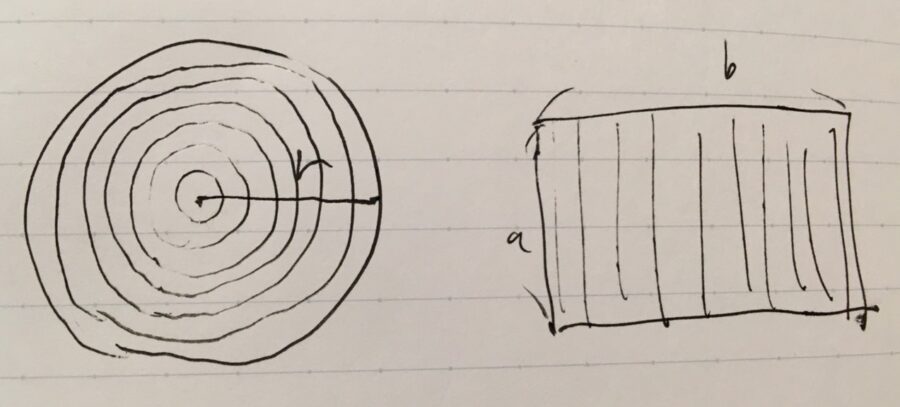



円の面積 円周 球の体積 表面積の公式の覚え方 微積分 趣味の大学数学




簡単公式 3分でわかる 半球の体積の求め方 Qikeru 学びを楽しくわかりやすく
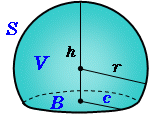



一部が欠けた球の体積 高精度計算サイト




中学数学 球の体積の求め方の公式を1発で覚える方法 Qikeru 学びを楽しくわかりやすく
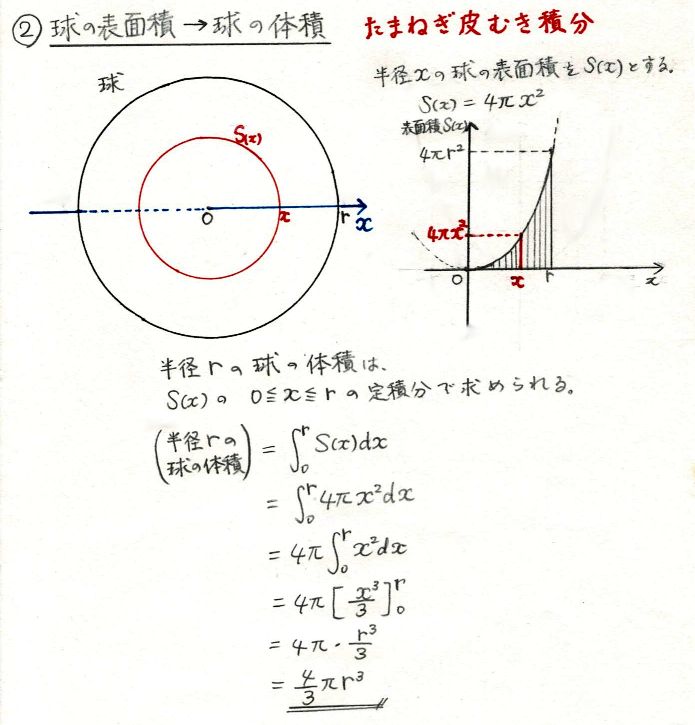



数学 円と球の公式を 微分 積分 で求める 温故知新ラーニング 楽天ブログ




数学 円と球の公式を 微分 積分 で求める 温故知新ラーニング 楽天ブログ



球とは 体積 表面積の公式や求め方 証明 積分 と計算問題 受験辞典



Search Q E5 86 86 E6 9f B1 81 Ae E4 93 E7 8d Tbm Isch




球の体積 表面積 中学生にも納得のいく方法で 積分でも出します Youtube



至急 球を4等分したものの体積と表面積の求め方をを教えてください Yahoo 知恵袋




球の表面積の求め方 その3 感じる科学 味わう数学




体積の求め方 計算公式一覧
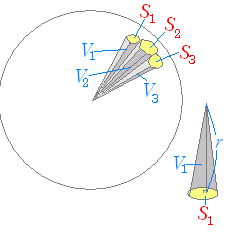



例題対比 球の体積と表面積




球の表面積 体積 中学数学から大学の数学まで広く眺める 身勝手な主張



477 Abacadsqrt21 cddb6 Descubre Como Resolverlo En Qanda




球の体積の求め方を教えていただけませんか よろしくお願いしますm M Clear




球の表面積と体積の公式 数学fun



球の体積の求め方の公式の絶対に忘れない覚え方を教えます Studyplus スタディプラス




球体の体積 中学生に分かるように真剣に考えてみた うちーノート




球の体積と表面積 公式と計算問題と証明 Irohabook




中1 中一数学 球の表面積と体積 中学生 数学のノート Clear




初めて知った 球 の表面積の秘密 数学の美しさ 花と器 Coffee Break100のブログ




球の体積の求め方 公式の覚え方と計算方法まとめ 中学数学 理科の学習まとめサイト




円柱の水槽に球を入れる問題 苦手な数学を簡単に




2次元 3次元 4次元 5次元 高次元 の球の体積 宇宙に入ったカマキリ



Yogb6 Tjpto Wm




中1数学 球 例題編 映像授業のtry It トライイット




球の体積と表面積の公式と覚え方を一目でわかるように図を用いて解説します 練習問題付き 高校生向け受験応援メディア 受験のミカタ




簡単公式 3分でわかる 半球の体積の求め方 Qikeru 学びを楽しくわかりやすく




面積 体積 計算ツール 福井鋲螺株式会社 冷間鍛造 冷間圧造 ヘッダー加工の専門メーカー リベット 特殊形状パーツおよび省力機器の製造 販売




Mathematics 球の体積と表面積を求める公式 働きアリ




球の体積と表面積 Youtube




球の表面積の公式について みたにっき はてな




中学数学 球の体積の何で 数樂管理人のブログ



1 この球の体積と円柱の体積の比を求めなさい 2 この球の表面積と円柱の Yahoo 知恵袋




立体の体積まとめ 角柱 円柱 角錐 円錐 球 A 教遊者




球の体積と表面積の求め方 公式を使う中学数学での計算 リョースケ大学



Q Tbn And9gcr6jkoybdanugf1fmicpptzy5auleu32fgwe6 X Jkyzlirf8w1 Usqp Cau




球に関する公式 理数系無料オンライン学習 Kori




球の体積と表面積の公式と覚え方を一目でわかるように図を用いて解説します 練習問題付き 高校生向け受験応援メディア 受験のミカタ




角錐 円錐の体積と表面積の公式 数学fun




これまでで最高の面積 球 の 体積 の 求め 方 最高のぬりえ



1 2cm 1cm Descubre Como Resolverlo En Qanda
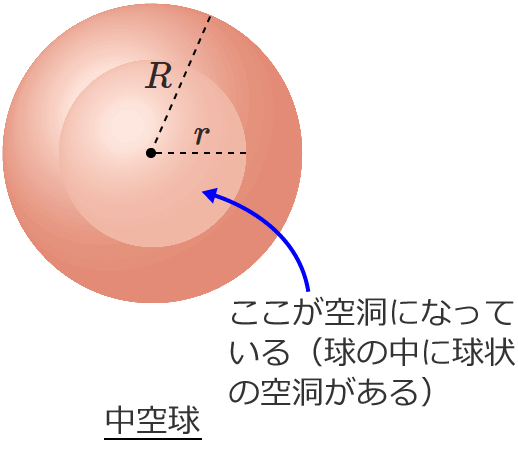



立体の体積を求める公式




球の体積 表面積 無料で使える中学学習プリント




球の表面積 体積 中学数学から大学の数学まで広く眺める 身勝手な主張




中1 中1数学 球の体積と表面積 中学生 数学のノート Clear



球の体積 高精度計算サイト




Formula85 球の表面積と体積 難関高校合格のための中学数学公式一覧 10秒で解けますか




半球の体積と表面積を計算する 具体例で学ぶ数学




球の体積と表面積の公式と覚え方を一目でわかるように図を用いて解説します 練習問題付き 高校生向け受験応援メディア 受験のミカタ




球の表面積の求め方 公式と計算例




3分で分かる 球の体積と表面積の公式 覚え方 語呂合わせ についてわかりやすく 合格サプリ




球の体積と表面積の公式と覚え方を一目でわかるように図を用いて解説します 練習問題付き 高校生向け受験応援メディア 受験のミカタ




中学数学 球の体積 表面積 中学数学の無料オンライン学習サイトchu Su



研究



球の表面積の公式の求め方




球の体積 表面積 公式の覚え方は語呂合わせで 問題を使って解説 数スタ




球冠 Wikipedia




球の表面積 体積 身勝手な主張




球の表面積と体積の公式 数学fun




数学講師必見 中学数学でも必須 球の体積 表面積の覚え方と導出まとめ 高校数学 塾講師ステーション情報局



16年前期 千葉県公立高校入試 数学 第2問 1 球の体積 表面積 解答 解説 船橋市議会議員 朝倉幹晴公式サイト



1




球の体積と表面積の公式と覚え方を一目でわかるように図を用いて解説します 練習問題付き 高校生向け受験応援メディア 受験のミカタ



球の表面積の公式の求め方




球の体積と表面積を積分で証明 高校数学の美しい物語



数学 球の表面積を積分で計算してもうまくいかない人へ



Q Tbn And9gcqqgrizekrnz Lytyjejolqml9yfhpazps6kyq0k Jpevu2dxgk Usqp Cau




中学1年生 数学 無料問題集 球の体積 おかわりドリル




中学数学 空間図形 体積の問題のコツ




球の表面積と体積の公式 数学fun



3分で分かる 球の体積と表面積の公式 覚え方 語呂合わせ についてわかりやすく 合格サプリ
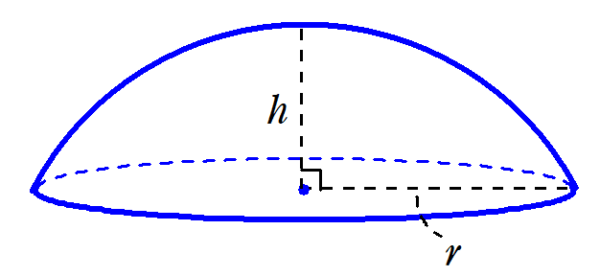



球欠と球冠 Fukusukeの数学めも



3分で分かる 球の体積と表面積の公式 覚え方 語呂合わせ についてわかりやすく 合格サプリ




中1 数学 6 5 球の体積 表面積 Youtube



球の体積 簡単に計算できる電卓サイト




球の体積 表面積 実験から公式を 授業実践記録 アーカイブ一覧 数学 高等学校 知が啓く 教科書の啓林館




球の表面積の公式と球の体積の公式 中学生の数学 要点 Yattoke 小 中学生の学習サイト




球の体積の公式を積分を使わず導く 中受でも出るかも 兄中学生活




体積 10 球と円柱の共通部分 怜悧玲瓏 高校数学を天空から俯瞰する




中学数学 球の体積の求め方の公式を1発で覚える方法 Qikeru 学びを楽しくわかりやすく




16年前期 千葉県公立高校入試 数学 第2問 1 球の体積 表面積 解答 解説 船橋市議会議員 朝倉幹晴公式サイト




初等幾何 球の表面積を求める 大人が学び直す数学




球の体積と表面積の公式をごちゃまぜにしない2つのポイント Qikeru 学びを楽しくわかりやすく




中1 中1数学 球の体積と表面積 中学生 数学のノート Clear




球の体積 球の表面積の公式の導出 積分 優技録




球の体積と表面積 数学i フリー教材開発コミュニティ Ftext



球の体積の求め方の公式の絶対に忘れない覚え方を教えます Studyplus スタディプラス




球の体積の公式 求め方や覚え方のコツを紹介するよ 中学や高校の数学の計算問題



0 件のコメント:
コメントを投稿