正方形や長方形の面積の求め方を「公式」に まとめたことを想起させ,三角形にも「公式」 があるのではないかという見通しをもたせる。 どのような求め方でも,三角形の面積は長方形の面積の半分に >(面積はあれでokですから、本題のほうは問題ありませんが。) >楕円の弧長は、「第2種楕円積分」であらわされます。 楕円の弧の長さの求め方を調べてみました。 今回は、横長の楕円と考えないと不都合だったので、 (x^2/27^2)+(y^2/^2)=1 実践!平米の出し方・求め方 実際にスケールやメジャーなどを使って部屋の大きさを計って、㎡に変換するにはどうしたら良いのか? 平米とは? まず平米を簡単に説明はすると、「1m×1m」です。平米を出したい部屋の床の縦×横を計算すれば良いだけです。

円の面積の求め方を一通り身につけたら 少し応用的な問題にも挑戦してみましょう 円の面積の応用問題をやってみよう 円の面積の もっと基本的な問題のノート例はこちらです 円の面積 数学ノート 学習ノート 学習
色々な面積の求め方
色々な面積の求め方-三角形の面積 ・正三角形の面積 1辺の長さを指定して、正三角形の面積を計算します。 ・三角形の面積(底辺と高さ) 底辺と高さから三角形の面積を計算します。 ・三角形の面積(2辺と間の角度) 2辺と間の角度から三角形の面積を計算します。円柱の底面積 S S は、 S = πr2 S = π r 2 で求められます。 よって、底面の半径 r r 、高さ h h の円柱の体積 V V は、次の式で求められます。




三角形の面積の求め方まとめ 数学の偏差値を上げて合格を目指す
三角形 (さんかくけい) の 面積 (めんせき) の求め方の 基本 (きほん) は「 底辺 (ていへん) × 高 (たか) さ ÷ 2」ですが、高さが分からないときに 他 (た) の 情報 (じょうほう) から面積を求める 公式 (こうしき) がいくつもあります。こうすることで、長方形の面積として求めることができます。 次の考え方でも平行四辺形の面積は、求められます。 動画作成協力・・動くイラストフリー素材 平行四辺形の面積の求め方を理解したら、 平行四辺形の面積を求める公式 を整理させてください。 公式の理解ができたら、公式を覚える練習をさせましょう。 公式 平行四辺形の面積=底辺×高さA = 面積 L = 弧の長さ α = 角度 (DEG) α = 角度 (rad) 弓形 A = 面積 L = 弧の長さ α = 角度 (DEG) α = 角度 (rad) 円 A = 面積 D = 外径 d = 内径 楕円 A = 面積 P = 円周(近似式) 円錐 V = 体積 A = 円錐面積 r = d/2 = 半径 三角錐 V = 体積 S = 角錐底面積 角錐
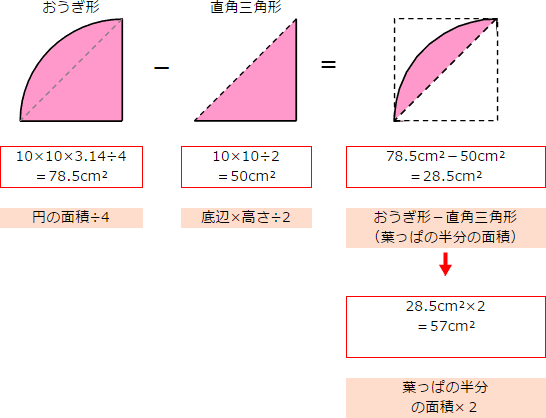
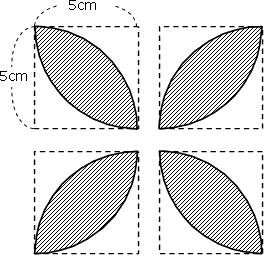
よって ア:イ=1:057 上の考え方を使うと下の正方形と色のついた部分の面積比も 1:057 になる。 正方形の面積=,10×10=100 (㎠) 100:面積=1:057 面積=57㎠ と求めるこ円を細かくおうぎ形に切って、交互に逆さまに並べていくと長方形になります 。 辺の長さは、短い方が円の半径、長い方は円周の半分(半径×314)になります。 短い辺(半径)と長い辺(半径×314)の長さを掛けて円の面積になるのです。体積・表面積 立方体の辺の長さから体積と表面積を計算します。 立方体の体積から辺の長さと表面積を計算します。 直方体の三辺の長さから体積と表面積を計算します。 四面体の6つの辺の長さから体積と表面積を計算します。 正四面体の辺の長さから体積と表面積を計算します。 正四面体の体積から辺の長さと表面積を計算します。 正三角柱の底辺と高さ
三角形の面積の求め方まとめ。タイプ別でわかる公式一覧 三角形の面積は「 \(底辺×高さ÷2\) 」という公式から求まりますが、この公式以外にも色々な方法で三角形の面積を求めることができます。面積の求め方 扇形 扇形の面積を求める公式は、次の通りです。 S = πr2 × x 360 = 1 2lr S = π r 2 × x 360 = 1 2 l r 中心角 x°、半径 r の扇形 ここで、S は扇形の面積、π は円周率、r は円の半径、x は中心角(単位「度」)を表します。 また、2行目の l は扇形の弧の長さを表します。 このページの続きでは、この 公式の導き方 と、 扇形の面積を求める計算問題の解き方四角形・三角形の面積/理解シート いろいろな台形の面積の求め方を教えて 無断複製・転載・翻訳を禁ず gakken b
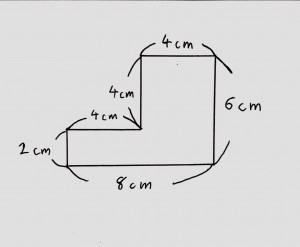



面積 体積を求める問題が苦手な子へ 小学生向け 愛知 岐阜の個人指導専門塾
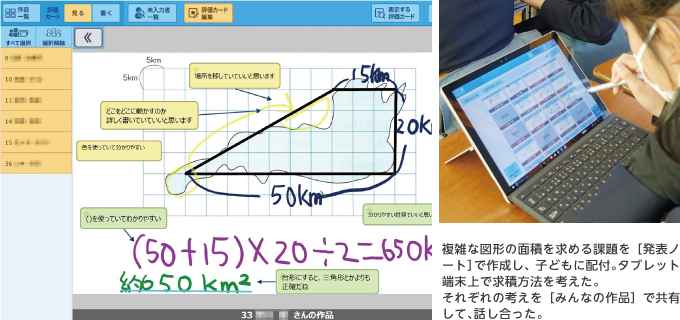



茨城大学教育学部附属小学校 学校とict sky株式会社 Ictを活用した学習活動をサポート
です。 ( π は円周率: π =←無限に長い小数になるからギリシャ文字 π で表すことになっている) 半円の面積は,円の面積の半分だから 3分の1円の面積は,円の面積の3分の1だから 4分の1円の面積は,円の面積の4分の1だから 一般に中心角の扇形の面積は,円の面積のx/360だから 例題1 半径がa (cm2)で中心角が45°の扇形の面積S (cm2)は 例題2なんと、3つの辺の長ささえ分かれば、面積が分かるのです。 「高さ」を測る必要もない、角度を調べる必要もない。 長さを測るものさしが1つあれば、三角形の面積をサクッと求められるのです(図3)。 たとえば、三角形の3つの辺が5mと3mと4mなら、 s = (534)÷2 = 6 s = ( 5 3 4) ÷ 2 = 6 T = √6(6−5)(6−3)(6− 4) = √6×1×3×2 = √36=6 T = 6 ( 6 − 5) ( 6 − 3) ( 6 − 4) = 6 × 1 円錐の表面積の公式を使うのもokですが、ここでは定石通り、底面積と側面積を求めてから円錐の表面積を求めてみます。 まず、 底面積 =3 2 π =9π・・・① ですね。 次に、側面積を求めます。まず、円錐の展開図を考えて、下の図におけるlを求めます。




中1数学 円柱 円すいの体積の求め方がサクッとわかる 映像授業のtry It トライイット
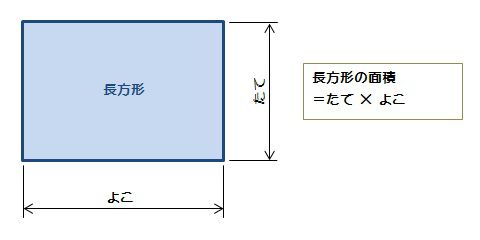



長方形の面積 算数の公式覚えてますか
動画一覧や問題のプリントアウトはこちらをご利用ください。ホームページ → http//19chtv/ Twitter→ https//twittercom/haichi_toaru小学1年生の算数 いろいろな形形づくり・形の弁別・立体の面を写した絵描き遊び 練習問題プリント 小学1年生算数「いろいろな形」の練習問題プリントです。 身近な物で、円柱、球、三角柱、直方体などの形の特徴を知り、箱や色板、ひごなどを用いた形づくり、立体の面を写した絵描き遊びなどの問題を通して様々な形の違いを学びます。 (プリント8枚)3 円の面積(2) この章では、別のやり方で、半径r の円の面積S(r) を求めてみましょう。以下では、 議論の本質を明確にするために、r =1の場合に説明します。 一般のr の場合には、どの ように議論を修正すべきかを考えてみてください。
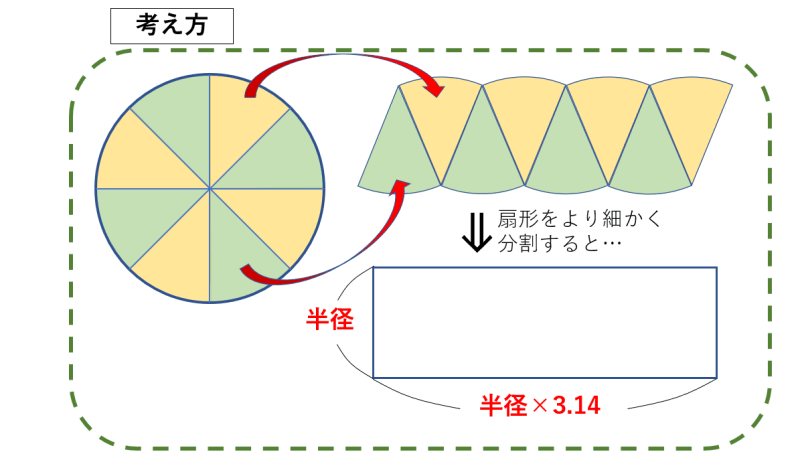



小学算数の面積の求め方と公式一覧 四角形 長方形の性質や円の計算方法まで解説 学びtimes



H21面積
れば,公式をつかって色々な図形 の面積を求めることができるね。 2 三角形abcの面積を求めましょう。 まず、緑の三角形の面積は、 次に、黄色の三角形の面積は、 最後に、二つの三角形の面積をたして、 =105 答えで求められます。 ②正方形の面積の求め方を考えさせます。 ↑の正方形は たてもよこも1cmが4つで4cmです。 面積は 16 です。 つまり 正方形の面積は 一辺の長さ×一辺の長さ で求められます。 面積の公式 長方形の面積 たて×よこ 本記事では、 だれでもできる屋根面積の簡単な求め方 をご紹介します。 メジャーが1つあれば 、簡単に屋根面積は測れます。 屋根のリフォームを検討されている方は、ぜひご自宅の屋根面積をはかってみてください。



台形とは 定義や公式 面積の求め方 面積比の計算問題 受験辞典
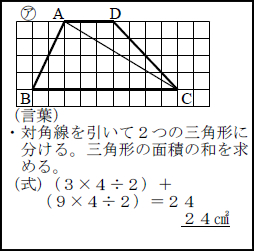



第5学年 面積 台形 私の実践 私の工夫アーカイブ一覧 授業支援 サポート資料 算数 小学校 知が啓く 教科書の啓林館
台形の面積 台形の高さ・面積(4辺の長さから) 台形の1辺・面積(3辺の長さと高さから) ひし形の面積 平行四辺形の面積(底辺と高さから) 平行四辺形の面積(2辺と夾角から) 円に内接する四角形の面積(4辺から) 四角形の面積(4辺と対角の和から)小学5年生 算数<11月>台形の面積/いろいろな図形の面積割合・百分率の意味と求め方 練習問題プリント 台形の面積、文章題、色々の図形の面積、文章題、割合・百分率、文章題 三角形の面積と,底辺と高さの関係について考える。 9 台形の面積の求め方を考える。 10 本時 平行四辺形を用いた倍積変形の方法をもとに、台形の面積を求める公式をつくる。 11 ひし形の面積の求め方を考える。 ひし形の面積を求める公式をつくる。 12
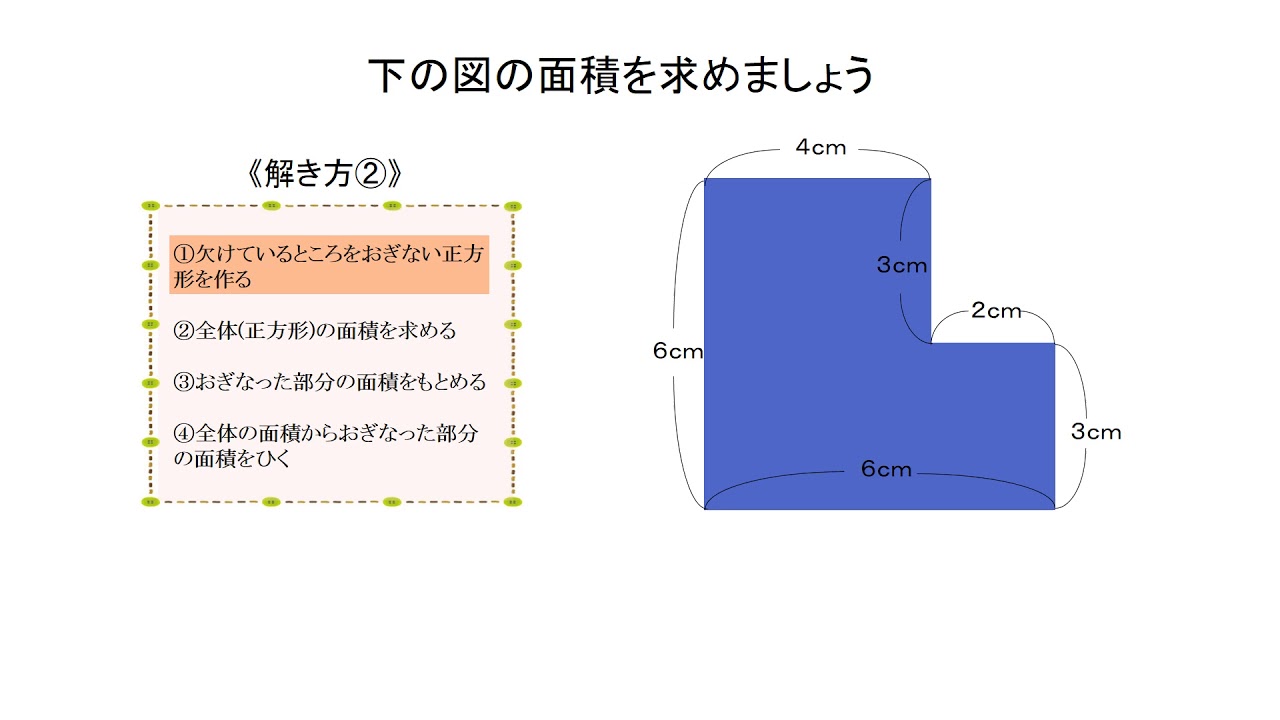



小4 面積の求め方の工夫 日本語版 Youtube




面積の求め方 算数の教え上手 学びの場 Com
まず、対角線で2つの三角形に分割する考えを取り上げます。 三角形ADB及び三角形ADCは辺ADを底辺とし、また、高さが三角形の外にある図形となるため、前時までの学習を振り返りながら確認します。 そして、2つの三角形の面積の求め方をひとつの式で表し、板書に残しておきます。 次に、平行四辺形に変形する考えを取り上げます。 移動する過程は、デジタル 問題 (正方形、長方形、平行四辺形、台形、ひし形、三角形、円を提示する) 面積の求め方が分かっている図形はどれでしょう。 四角形や三角形は求めることができます。 円はまだ学習していません。 これまでの面積の学習を生かして、円の面積の 平行四辺形の面積=底辺×高さ ひし形の面積=対角線×対角線÷2 台形の面積= (上底+下底)×高さ÷2 三角形の面積=底辺×高さ÷2 円の面積=半径×半径×円周率 (314) おうぎ形の面積=半径×半径×円周率×中心角/360° 公式の成り立ちから知りたい人や公式がまだ曖昧な人は こちらの記事 を読んでから、これから解説する問題に取り組んでください。 中学受験 算数




体積 表面積まとめ記事 いろいろな図形の求め方を一気に学べる 高校生向け受験応援メディア 受験のミカタ
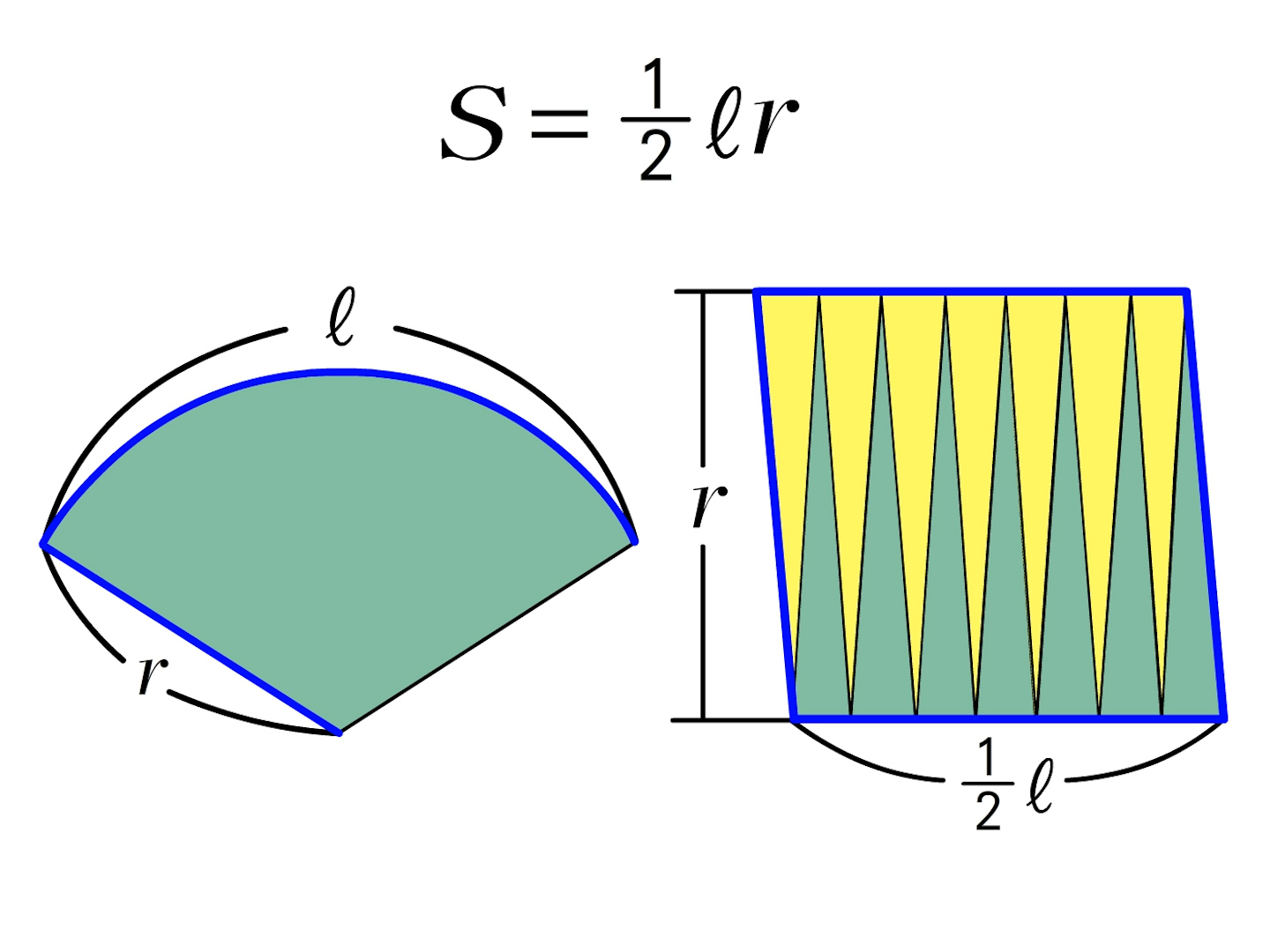



1年 おうぎ形の面積 数学イメージ動画集 大日本図書
三角形の面積のいろいろな表し方についてまとめました. (底辺)× (高さ)÷2 底辺を x x , 高さを y y とすると,三角形の面積 S S は次のように表せる. S = 1 2xy S = 1 2 x y この公式は、これまでに説明してきた求め方にしたがうことで簡単に導くことができます。 (底面の円の面積)=(半径)×(半径)×(円周率)=r × r × π= πr 2 (円柱の体積)=(底面の円の面積)×(高さ)=πr 2 ×h= πr 2 h




円の面積 練習応用 Youtube
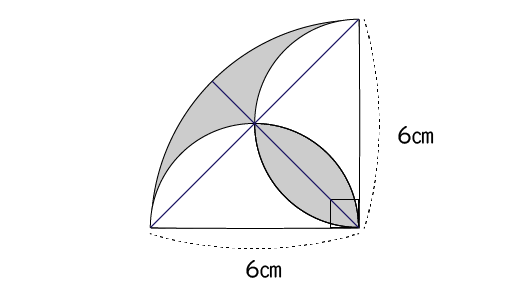



中学1年生数学 複雑な面積の求め方 長野地区 Itto個別指導学院 長野市の学習塾




台形の面積は公式が分からなくても大丈夫 対角線を引いたり等積変形を利用したりする求め方とは みけねこ小学校




小学算数の面積の求め方と公式一覧 四角形 長方形の性質や円の計算方法まで解説 学びtimes




この図形の面積の求め方を教えてくださいm M Clear
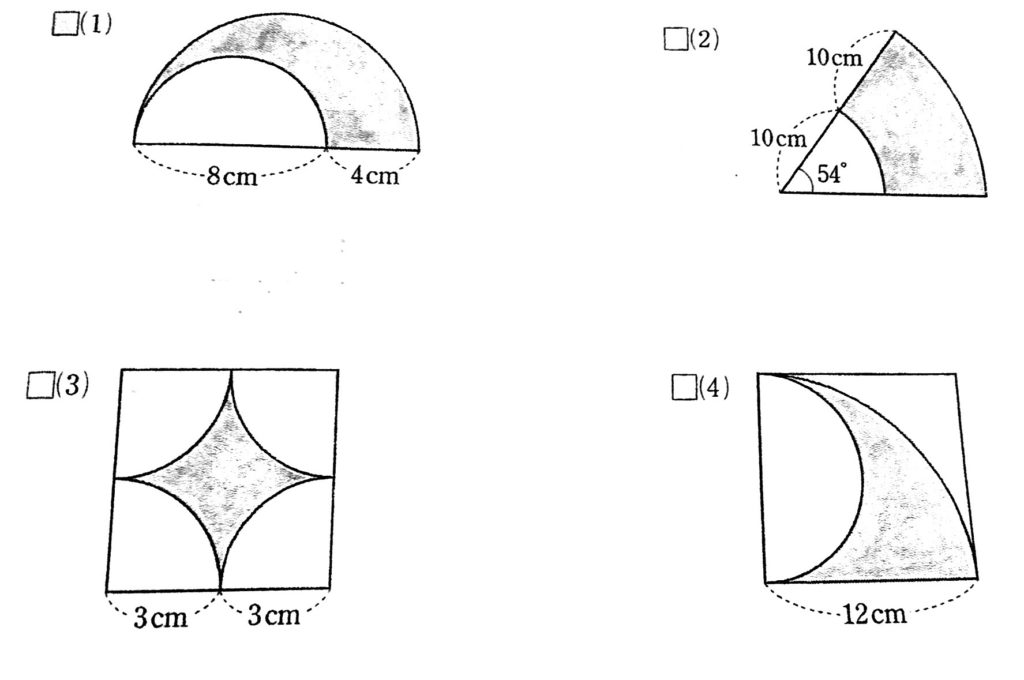



おうぎ形の応用 影の部分の面積 周の長さの求め方 数スタ




台形の面積の求め方 公式が誰でも一目でわかる 練習問題付き 高校生向け受験応援メディア 受験のミカタ




たこ形の面積の求め方を考えよう 5年算数 茎崎学園 つくば市立茎崎第二小学校




台形の面積の公式 小学生に教えるための分かりやすい解説 数学fun




ひし形の面積の公式 小学生に教えるための分かりやすい解説 数学fun




算数 小4 41 面積の求め方のくふう Youtube



4 8 長方形の中の複雑な斜線の部分の面積を求めるには さんすうがく パート 2
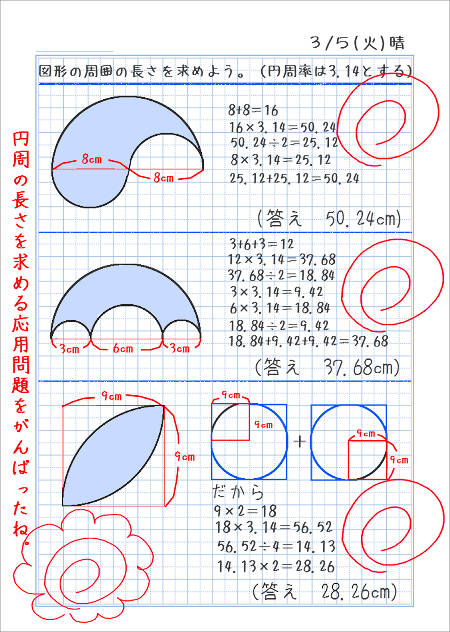



円周の長さの問題をもっと解いてみよう 家庭学習レシピ
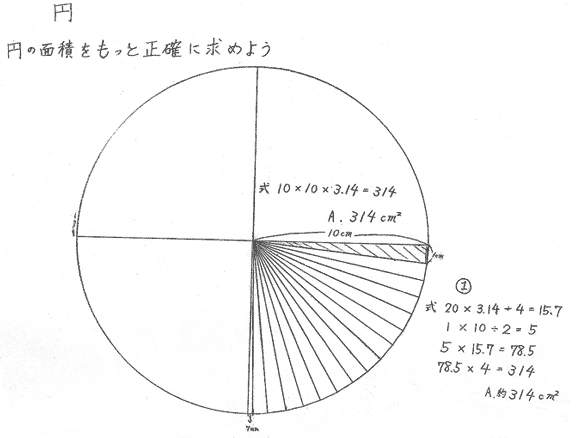



実践記録算数5年
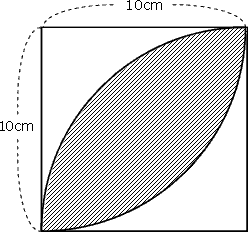



面積の求め方 算数の教え上手 学びの場 Com
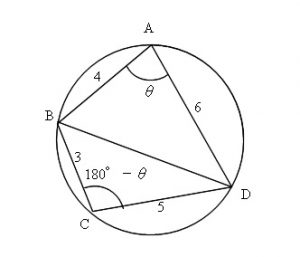



円に内接する四角形の面積の求め方と定理の使い方




円錐の表面積や体積の求め方 すぐ分かる方法を慶応生が解説 高校生向け受験応援メディア 受験のミカタ




台形の面積の求めかたは 忘れても大丈夫 公式は自分でつくろう



小学校で習うひし形の面積の求め方 対角線を使った公式で求められる理由 みけねこ小学校




平行四辺形の面積の求め方 公式と計算例
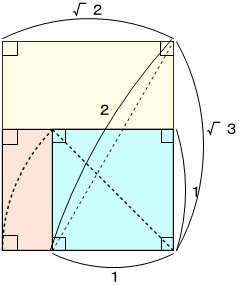



長方形の面積を求める公式の数学的な意味 Note Board



1




小学生 面積の求め方のノート一覧 Clear




長方形の面積の求め方 簡単な計算問題で公式を覚えよう 中学や高校の数学の計算問題
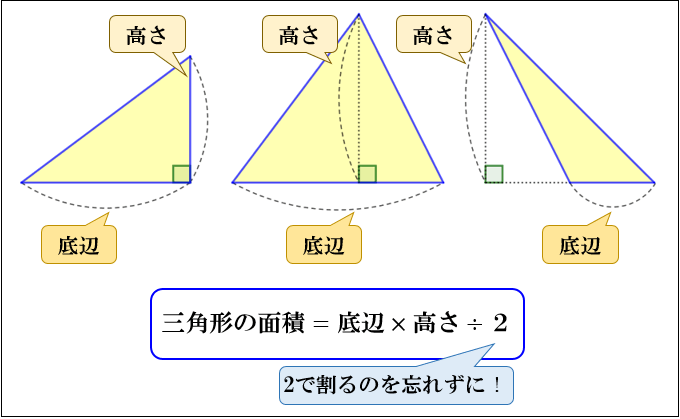



三角形の面積の求め方 なぜ底辺 高さ 2で求まるのか アタリマエ




円の面積の求め方を考えよう 小学校6年生の算数教材から 身勝手な主張



正三角形の面積 高さ 辺の長さの計算機 公式を使った求め方も紹介 やまでら くみこ のレシピ




面積の求め方 計算公式一覧



中受小5算数 いろいろな面積の求め方の問題です 添付画像が問題になります Yahoo 知恵袋
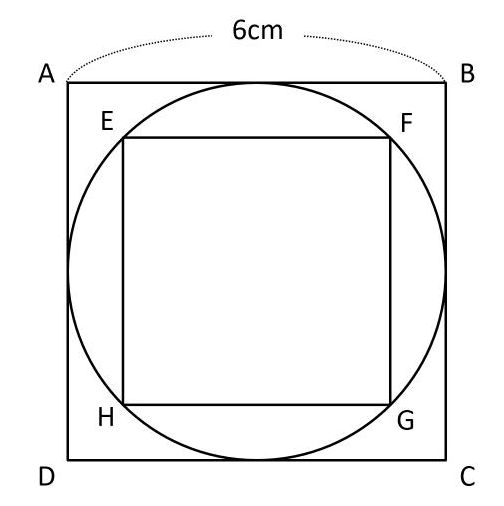



正方形の対角線の長さを求めたい 小学生が算数の知識を使ってどこまでできる 中学受験ナビ




図形の面積のいろいろな求め方 中3向けの動画です Studychannel スタディチャンネル 勉強が楽しくなる 学び 動画サービス



円の面積の求め方
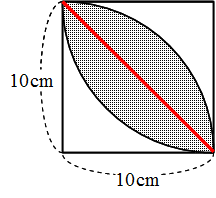



世界一やさしい 円の面積を求める問題の解き方 働きアリ



この四角形の中の三角形の面積の求め方をおしえてください A 長方形 Yahoo 知恵袋



6年算数 円の面積 2 わかる教え方




台形の面積の公式 ゆとり教育で求め方がわからない人は見て 中学や高校の数学の計算問題




高さがわからない台形の面積の求め方がわかる3ステップ Qikeru 学びを楽しくわかりやすく




三角形の面積の求め方とは Sinやベクトルを用いる公式も解説 小学生から高校生まで 遊ぶ数学



教育ソフト開発研究所 5年5巻
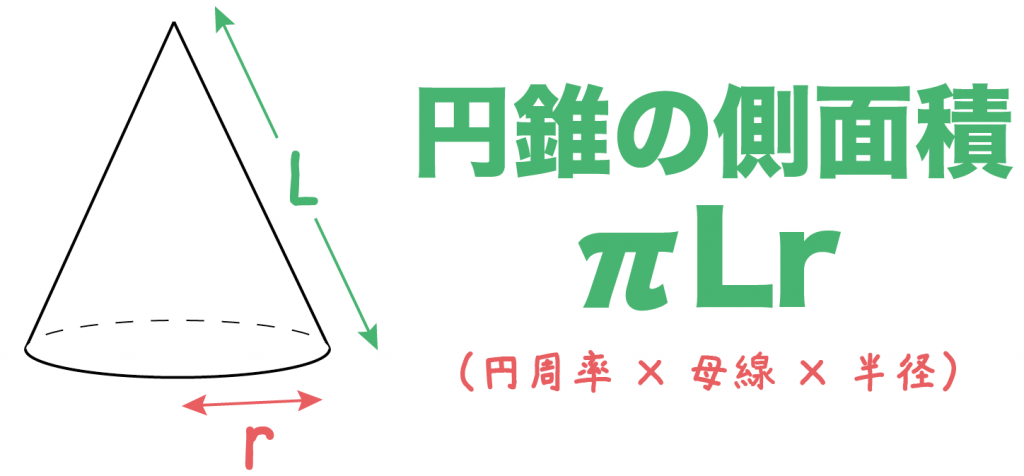



簡単公式 円錐の側面積の求め方がわかる3ステップ Qikeru 学びを楽しくわかりやすく




小学5年生 算数 11月 台形の面積 いろいろな図形の面積 割合 百分率の意味と求め方 練習問題プリント 栄光ゼミナール ちびむすドリル 小学生学習教材 スペシャルコラボ




平行四辺形の面積の求め方 公式と計算例



小学5年の算数の問題です 下図の斜線の面積の求め方を教えてください Yahoo 知恵袋




小5算数 図形の面積 指導アイデア みんなの教育技術
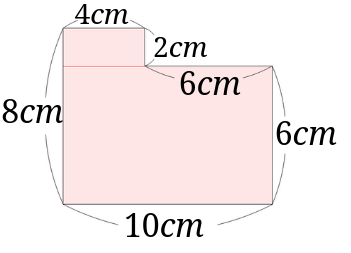



小学4年生で習う長方形や正方形の面積の応用問題を解説 みけねこ小学校




四角形の面積の求め方 公式とその仕組み 小学算数 アタリマエ




円の面積の求め方を自主学習ノートで復習しましょう 円の面積の基本的な練習問題 円の面積の求め方を確認しておき 学習ノート 学習 数学ノート
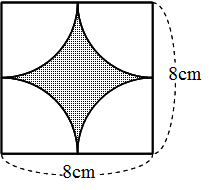



世界一やさしい 円の面積を求める問題の解き方 働きアリ




平行四辺形の面積の求め方 公式と計算例




三角形の面積の公式 小学生に教えるための分かりやすい解説 数学fun
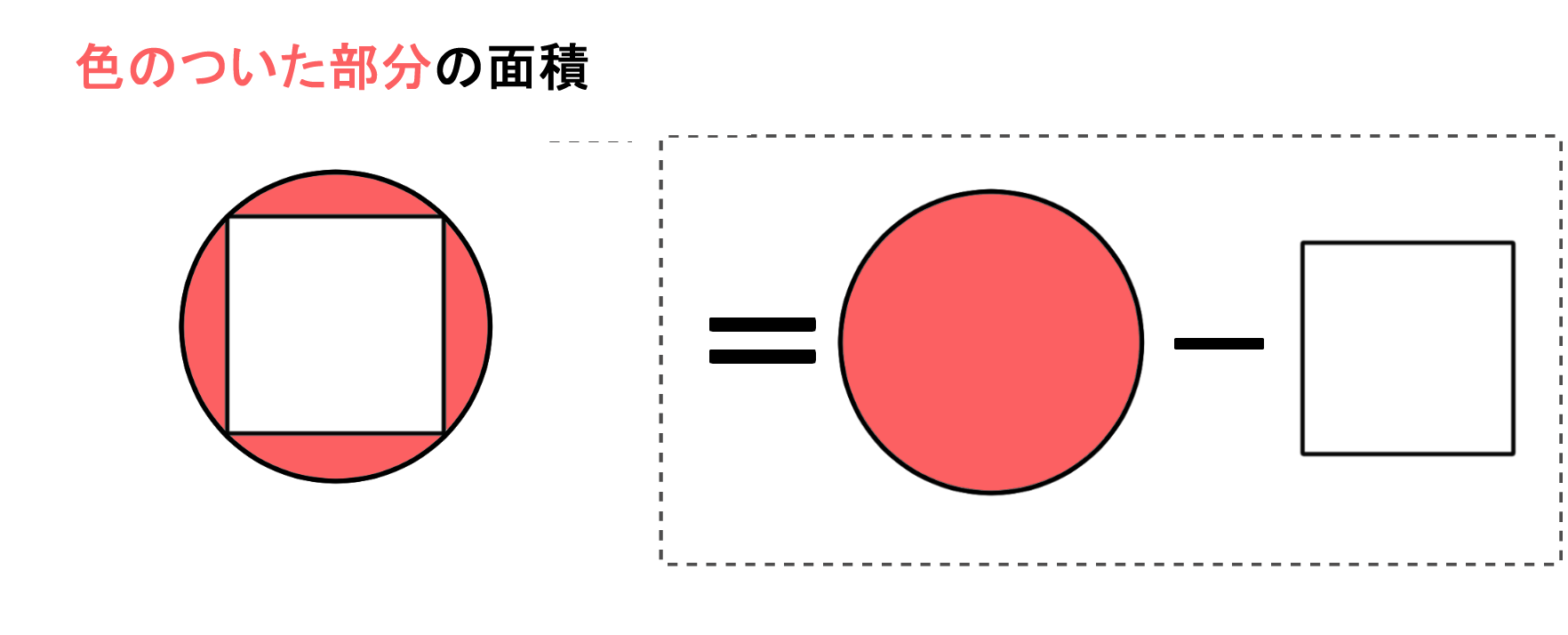



色のついた部分のへんな形の図形の面積を求める問題 バカでもわかる 中学数学




5年算数面積 教え方のポイント




平行四辺形の面積の求め方 公式と計算例



1




いろいろな面積を求める問題1 中学受験準備のための学習ドリル
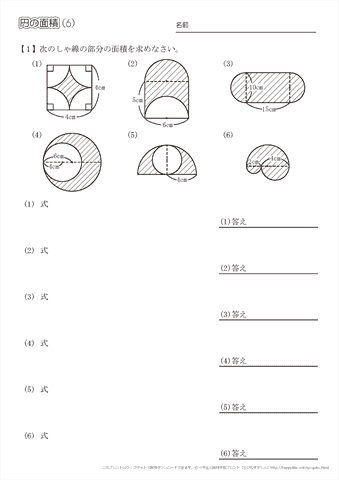



小学6年生の算数 円の面積 問題プリント ちびむすドリル 小学生



教材総合カタログ 19 小学校全教科




面積の求め方 計算公式一覧




高さがわからない台形の面積の求め方がわかる3ステップ Qikeru 学びを楽しくわかりやすく



2直角四角形の面積を求める極意 すぐるゼミ




簡単公式 ひし形 菱形 の面積を計算できる2つの求め方 Qikeru 学びを楽しくわかりやすく




小6 算数 小6 2 円の面積 応用編 Youtube




X軸の下の面積 を求める時の注意と 2つの曲線の間の面積 の求め方 高校数学の知識庫




扇形の面積の出し方と特殊な場合の公式 たぬぬ塾 中学校の先生たち




立体の表面積の求め方 直方体 円錐 円錐台 バカでもわかる 中学数学



図形の公式一覧 図形の面積と体積はこれでバッチリ 三重の個人契約家庭教師
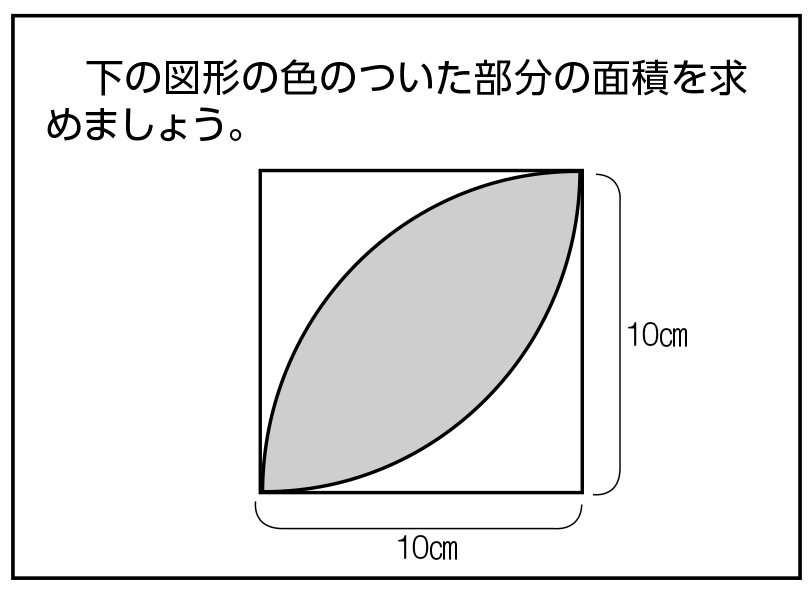



小6算数 円の面積 指導アイデア 2 みんなの教育技術




三角形の面積の求め方まとめ 数学の偏差値を上げて合格を目指す




面積の求め方 算数の教え上手 学びの場 Com




円の面積の求め方を一通り身につけたら 少し応用的な問題にも挑戦してみましょう 円の面積の応用問題をやってみよう 円の面積の もっと基本的な問題のノート例はこちらです 円の面積 数学ノート 学習ノート 学習




円とおうぎ形 いろいろな面積の問題 中学受験準備のための学習ドリル



面積の求め方 算数の教え上手 学びの場 Com
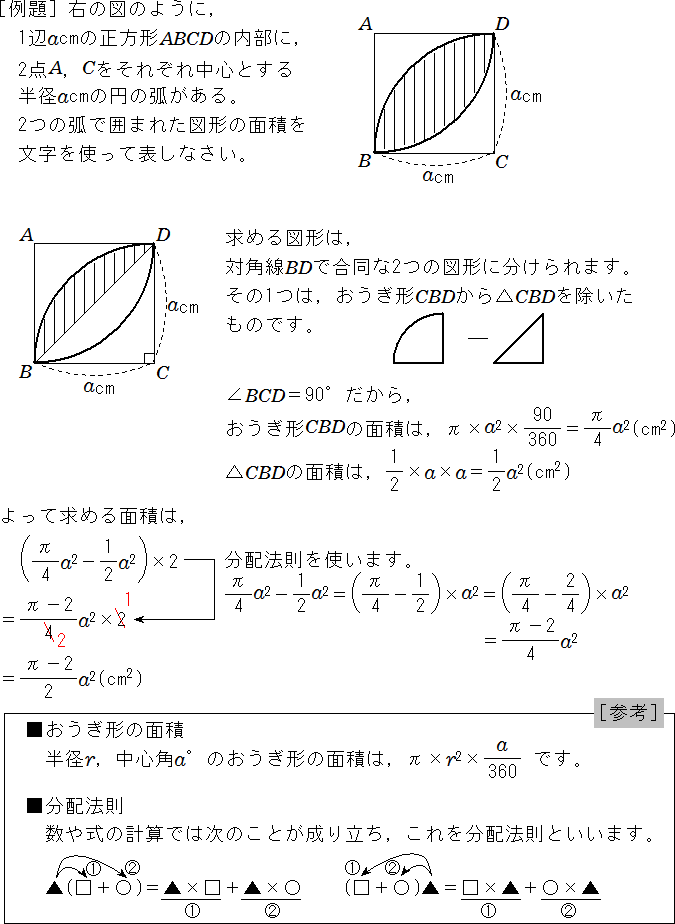



式の計算 文字を使った変わった図形の面積の求め方 中学数学 定期テスト対策サイト




小5 台形 面積の求め方 日本語版 Youtube
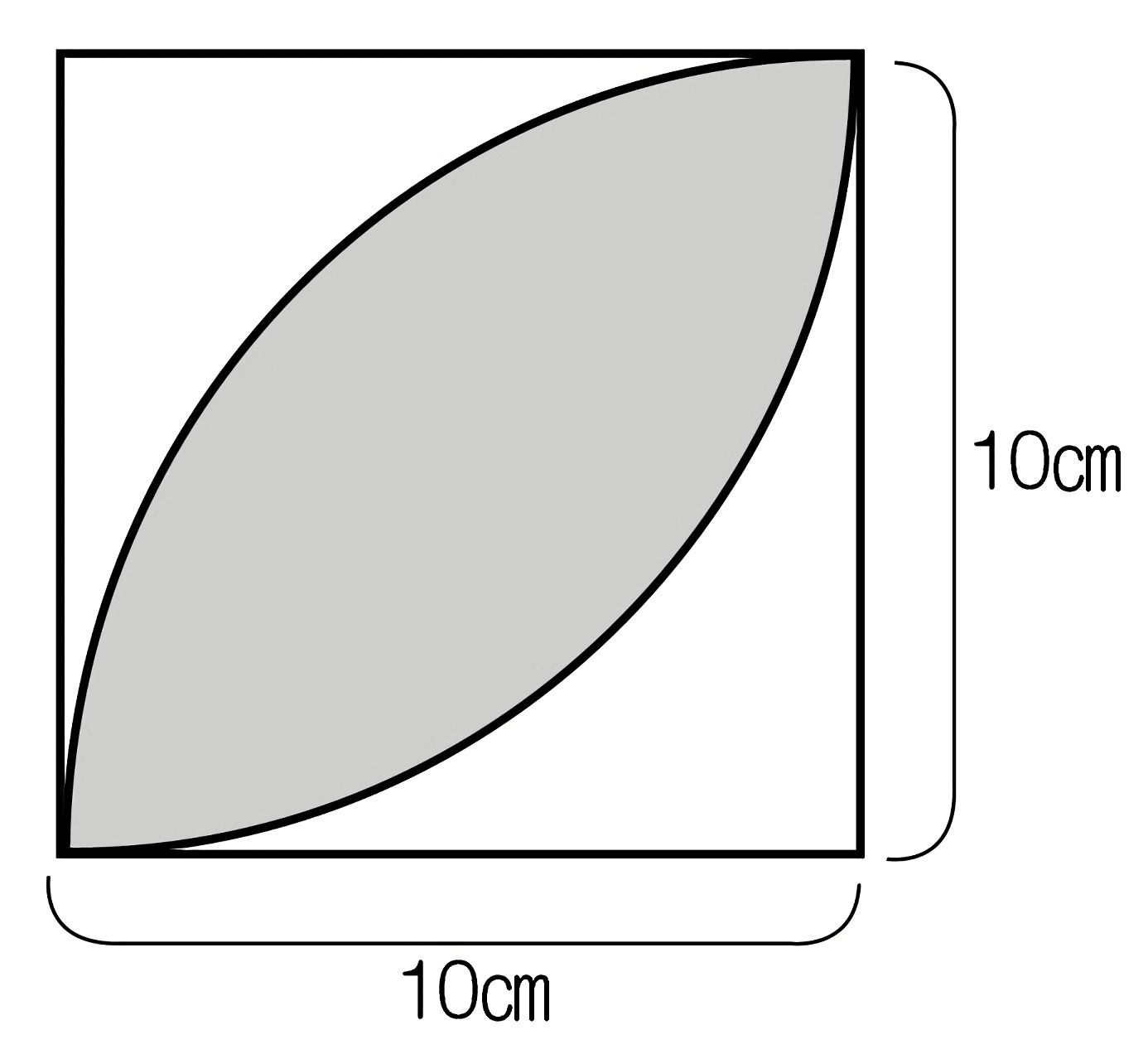



小6算数 円の面積 指導アイデア 2 みんなの教育技術
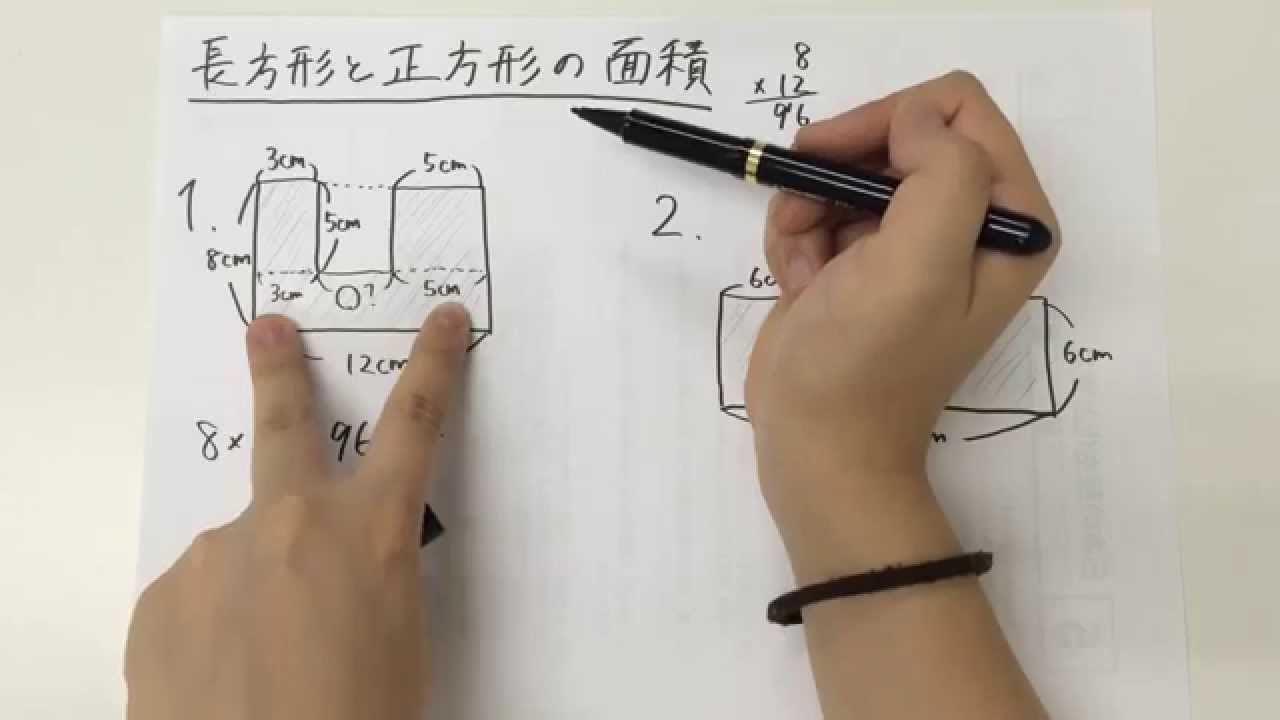



4年生 10 長方形と正方形の面積の求め方 Youtube



3




Descubre Como Resolverlo En Qanda



面積の求め方を考えよう 算数5年生の学習指導案 授業案 教材 Edupedia エデュペディア 小学校 学習指導案 授業案 教材




四角形の種類と定義 性質の違い 正方形 長方形 平行四辺形 ひし形 台形 数学fun



Www Saga Ed Jp Kenkyu Kenkyu Chousa H21 03shou San Jyugyou Documents Menseki Shidouan Pdf




円の面積はなぜ P R R なのか 公式の求め方を丁寧に解説 数学の面白いこと 役に立つことをまとめたサイト



6年算数 円の面積 2 わかる教え方
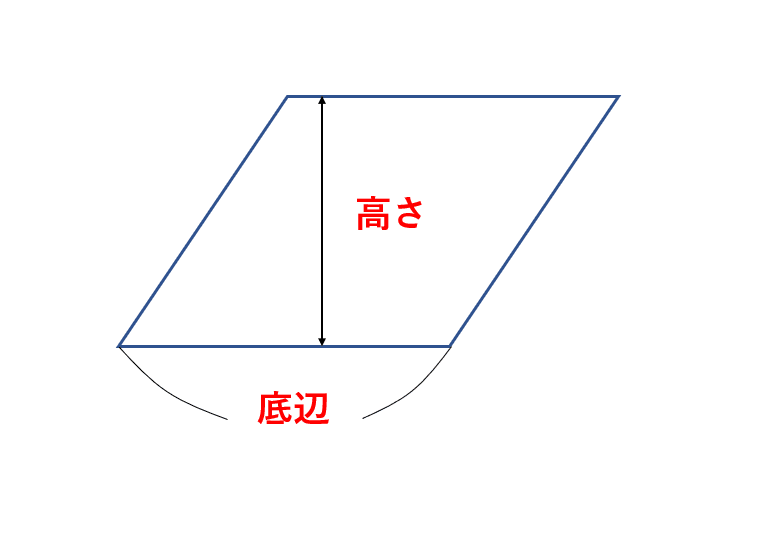



小学算数の面積の求め方と公式一覧 四角形 長方形の性質や円の計算方法まで解説 学びtimes




三角形の面積の求め方まとめ タイプ別でわかる公式一覧 アタリマエ




台形の面積の求め方 公式と計算例
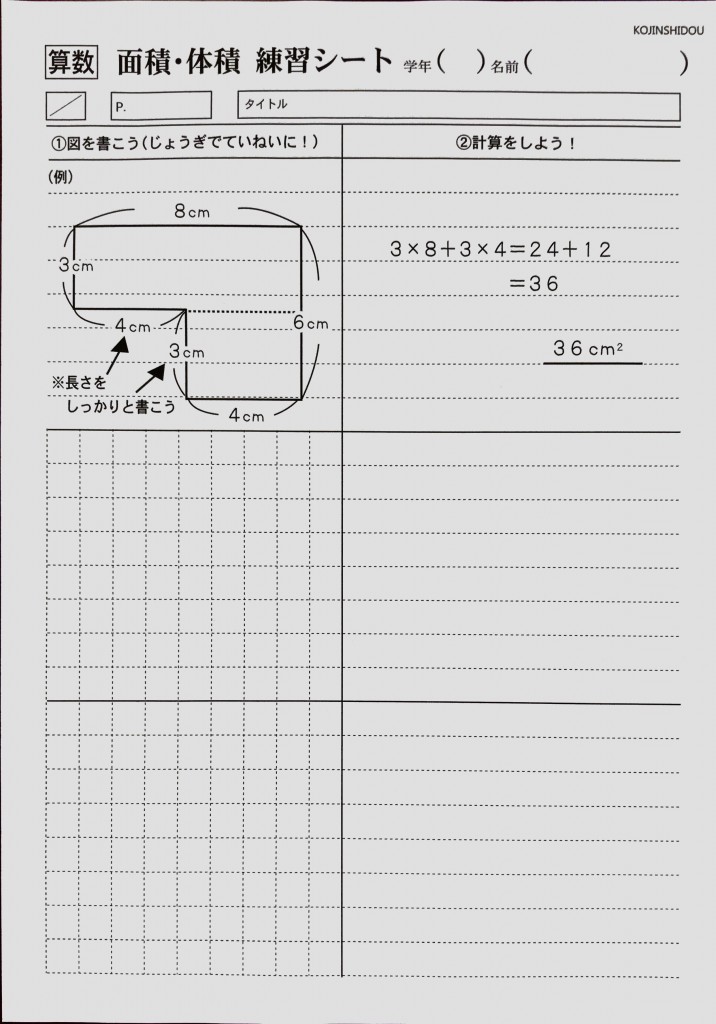



面積 体積を求める問題が苦手な子へ 小学生向け 愛知 岐阜の個人指導専門塾
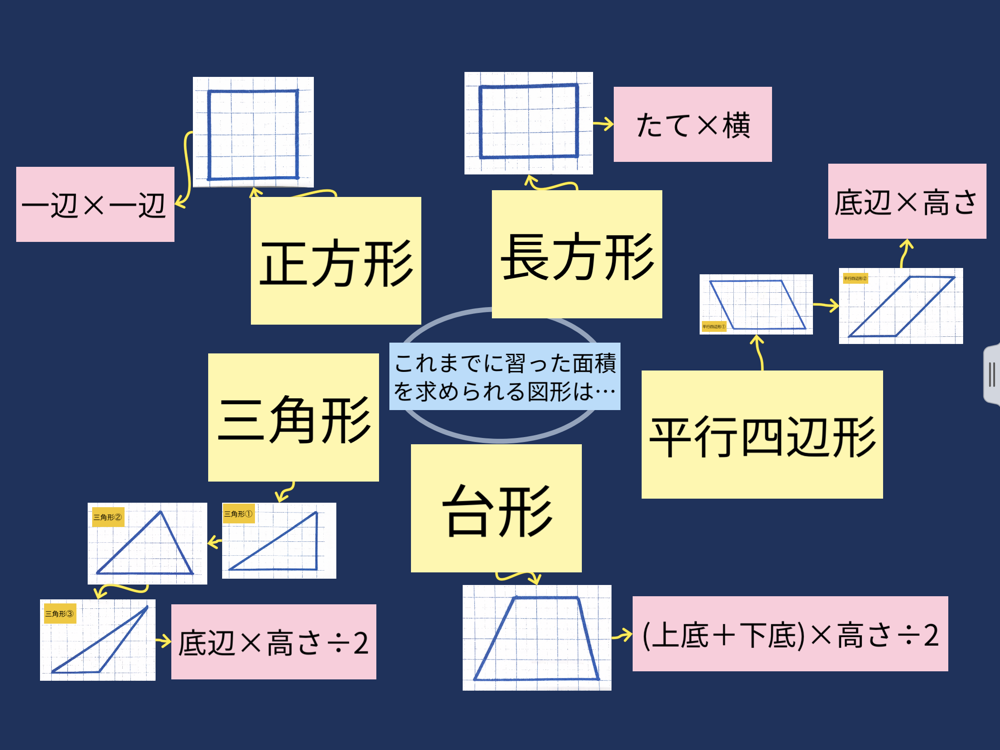



ロイロノート スクール サポートページ 小5 算数 ひし形の面積の求め方を考えよう 授業案 雲雀丘学園小学校 小田 剛士




ボード 子供の教育 のピン



面積の求め方 算数の教え上手 学びの場 Com




5年算数 面積 のわかる教え方 いっちに算数 のブログ




小5上第3回 いろいろな面積の求め方



0 件のコメント:
コメントを投稿