平行四辺形になることの証明 On Vimeo
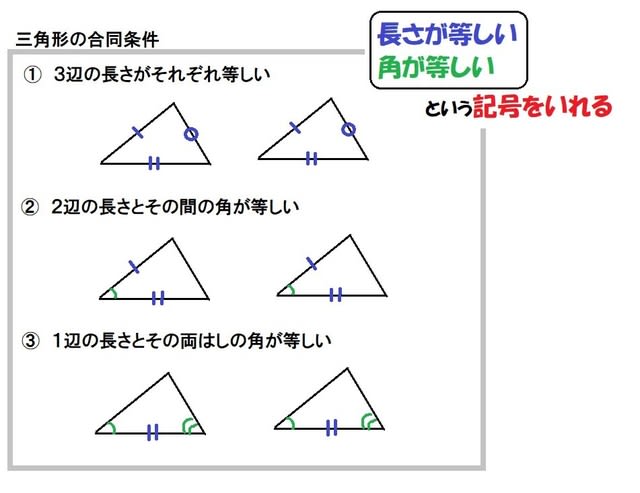
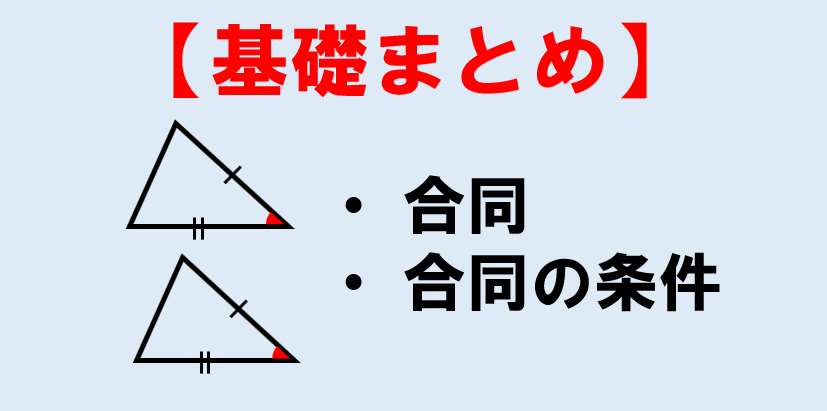
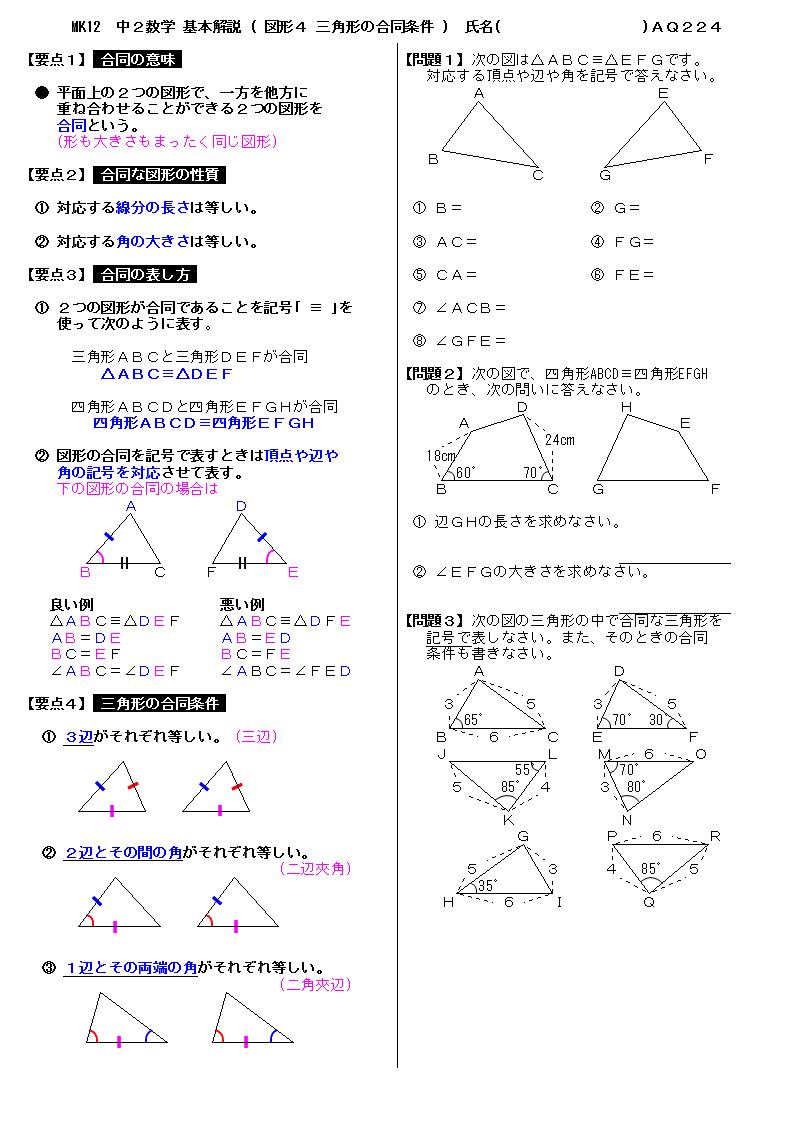
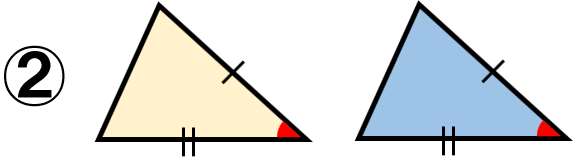
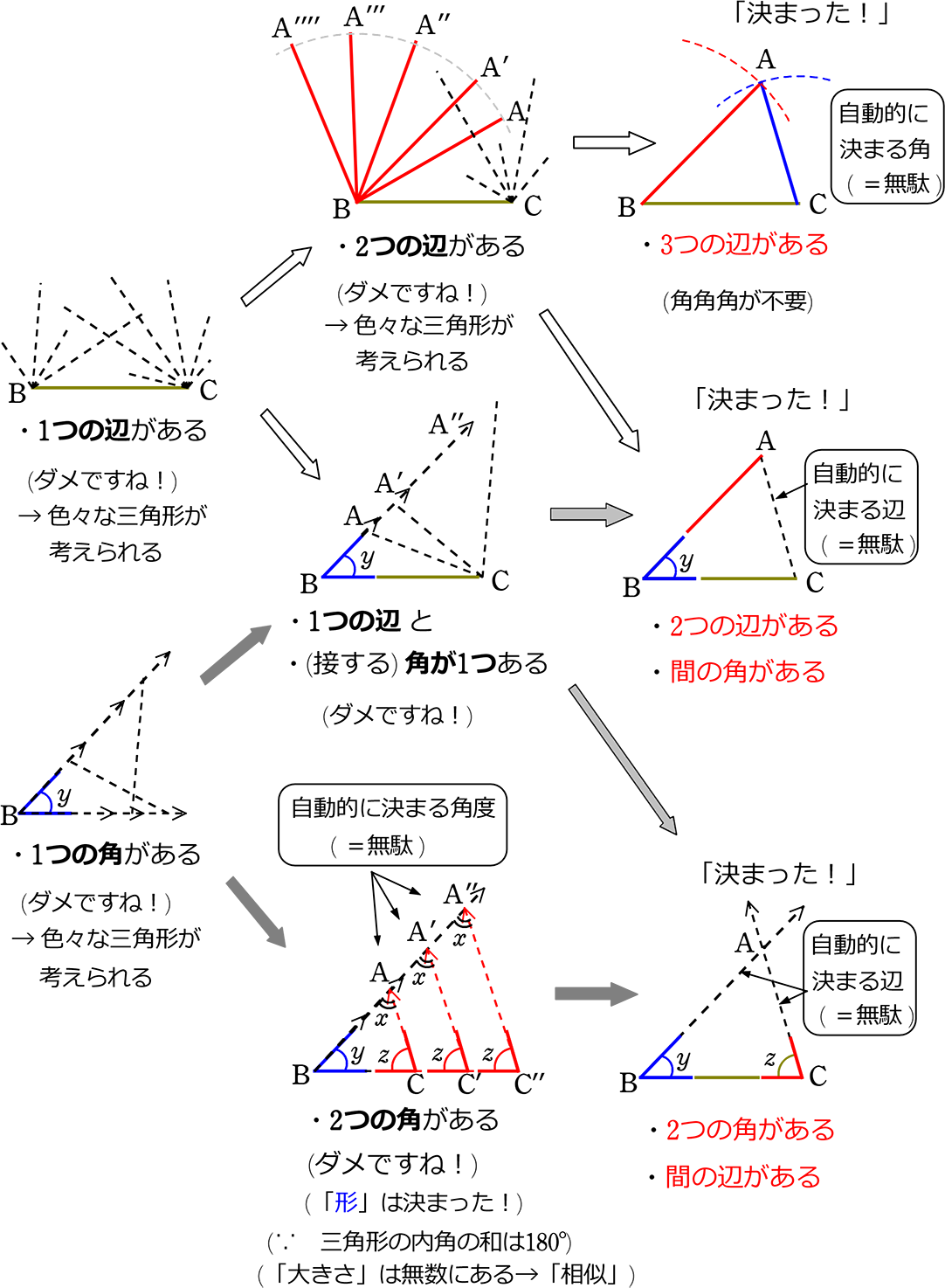
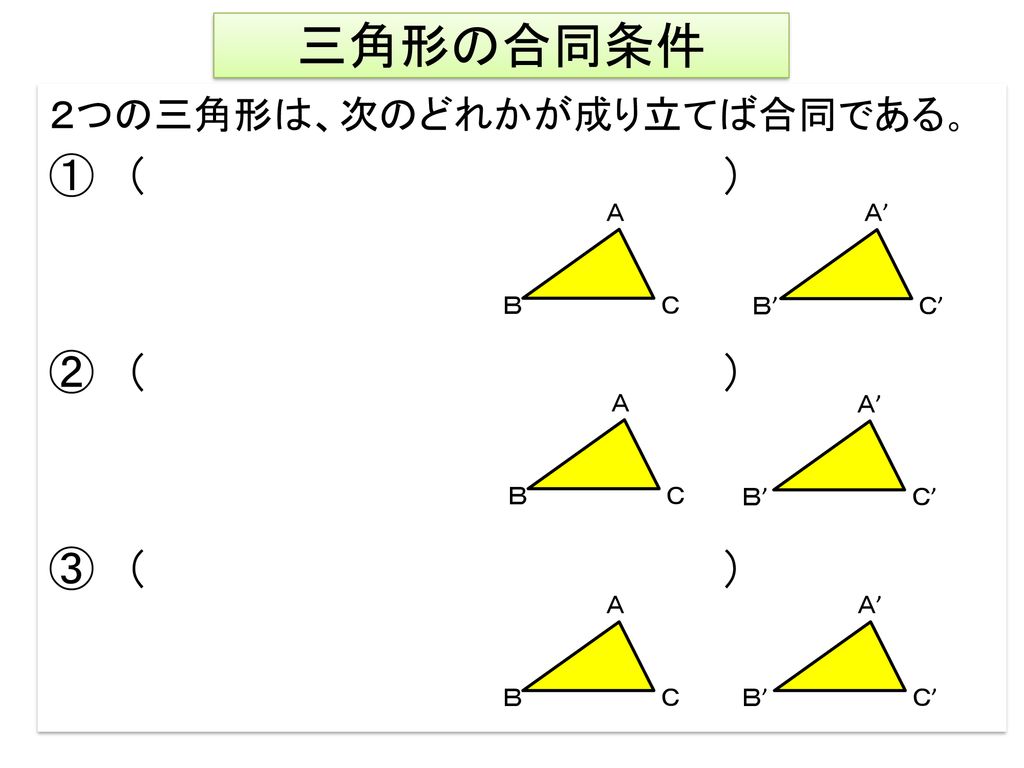
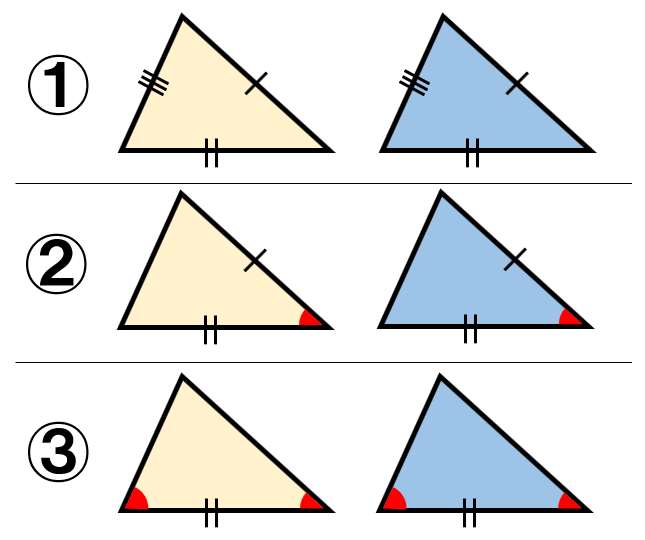
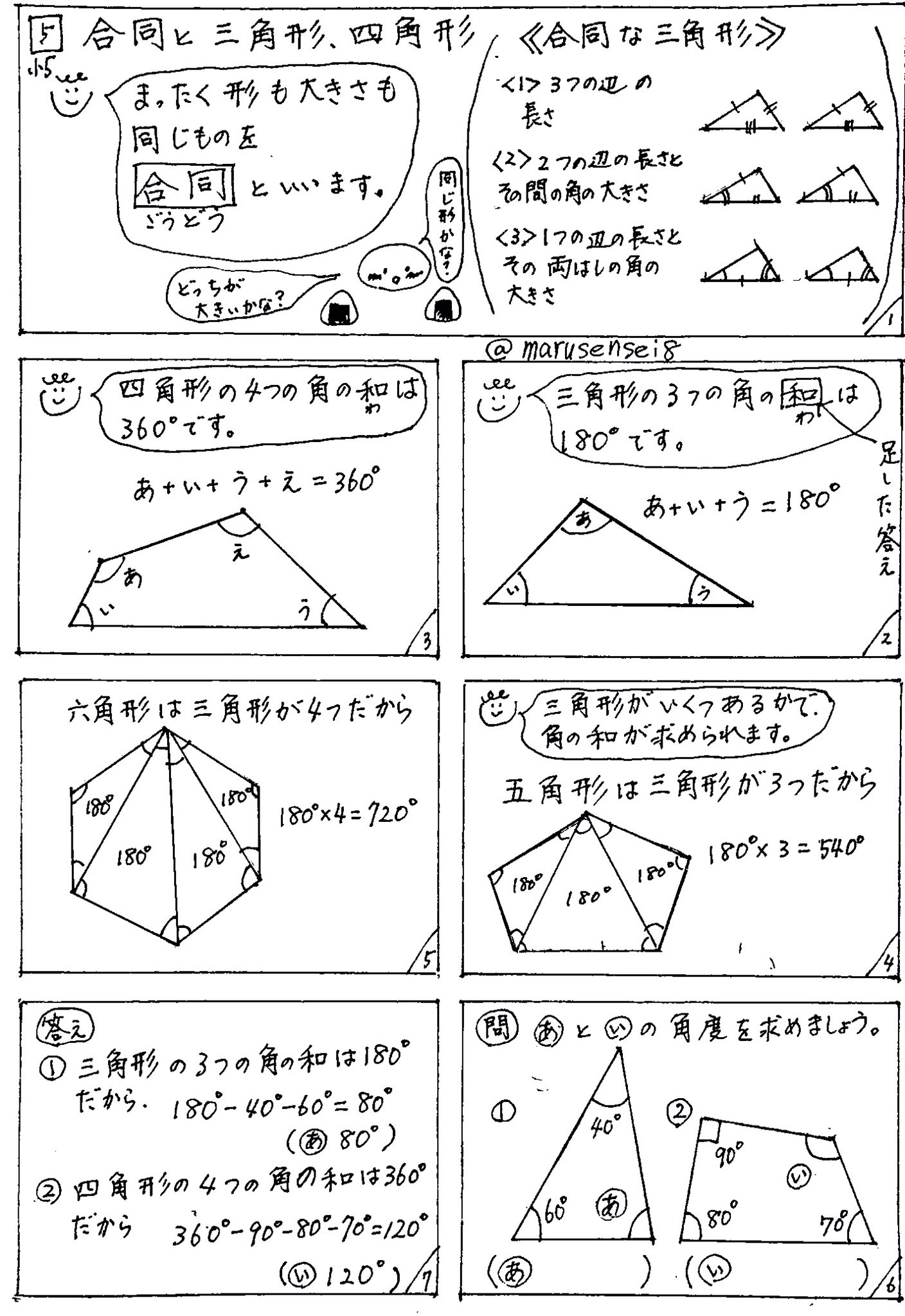
9/9/21 三角形の合同条件 3組の辺がそれぞれ等しい。 2組の辺とその間の角がそれぞれ等しい。 1組の辺とその両端(りょうはじ・りょうたん)の角がそれぞれ等しい。 ・小学5年生算数プリント一覧に戻る >教科書にはない「思考力ドリル」はこちら二つの多角形が合同であるためには、それらの辺の数が(従って頂点の数も)等しくなければならない。 n辺形が互いに合同となるための必要十分条件は、それらが持つ n 個の辺と n 個の角を「辺角辺角」のように順番に辿る(場合によっては一方を時計回りに、他方を反時計回りに辿る
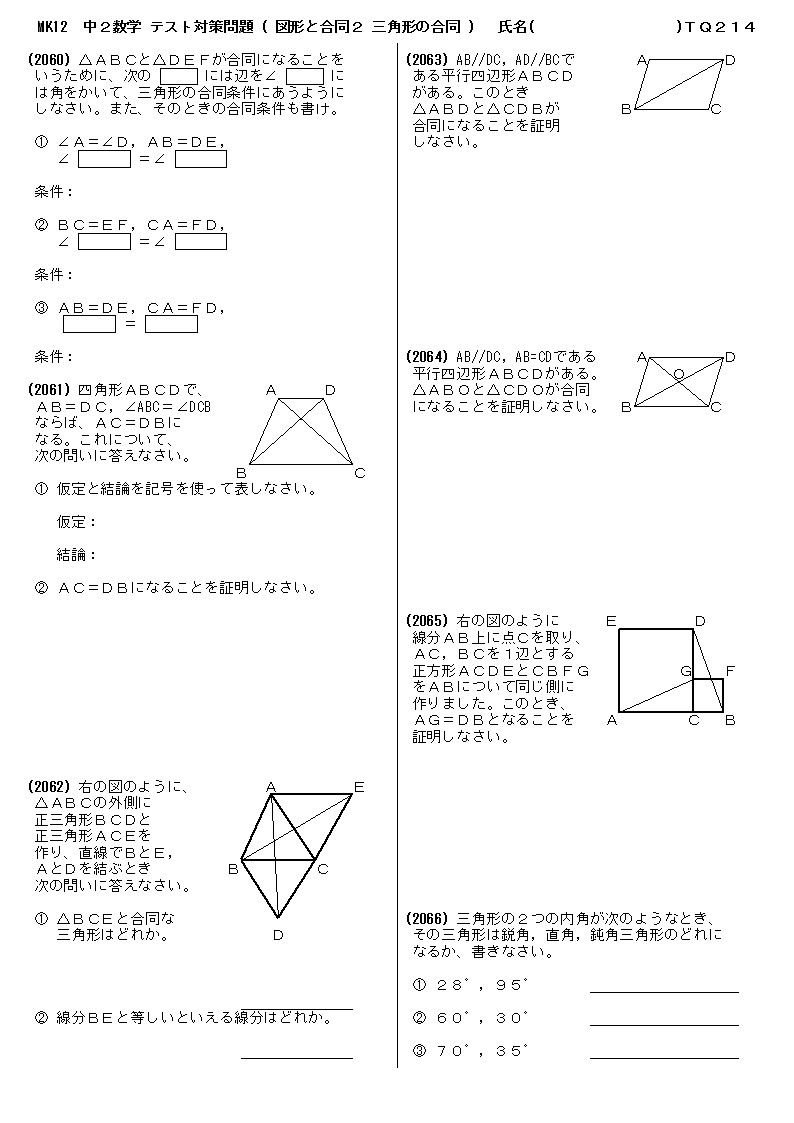
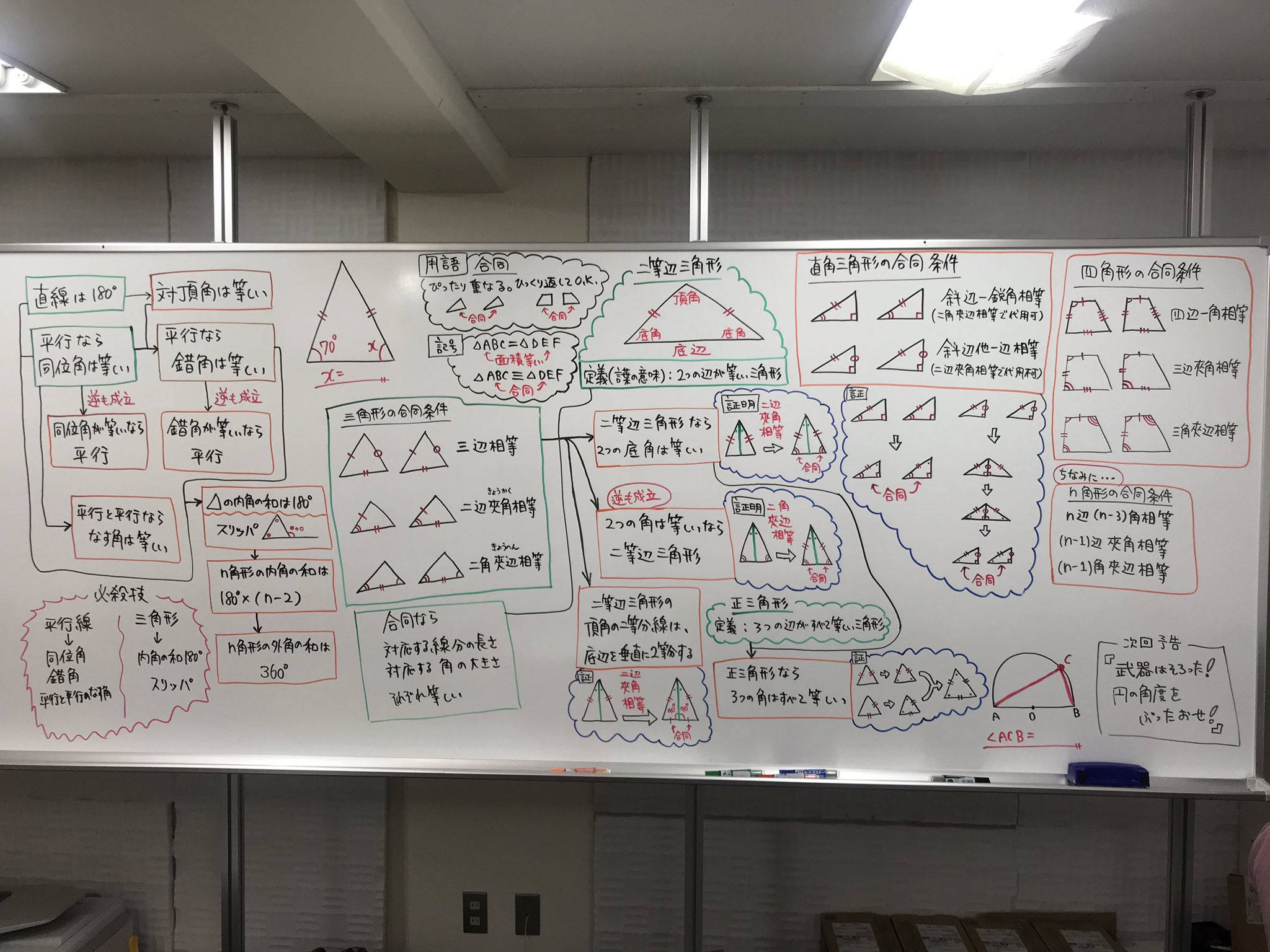
四角形 の 合同 条件
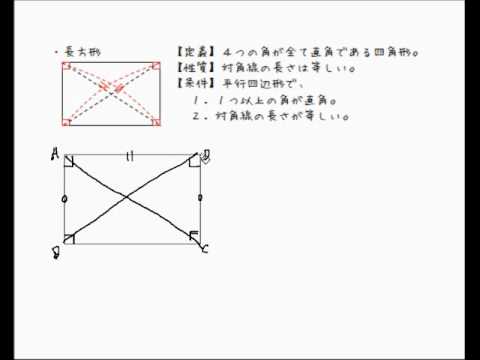
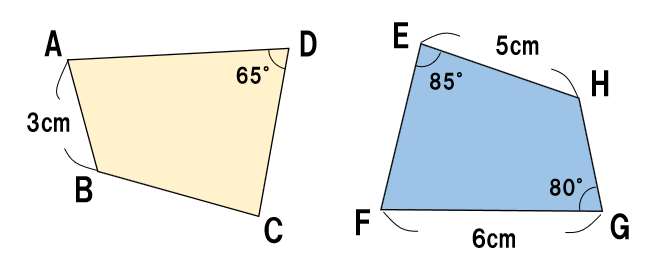
四角形 の 合同 条件-角度についての条件はなし 2 2 つの三角形があって、どちらも 1 1 辺は 10cm 10 c m で等しいんだ。 これだけの情報では、 2 2 つの三角形が合同であるとは確定できませんね。 「 1 1 つの辺が等しい」だけでは、合同が確定するためには、条件が少なすぎますContents 三角形の合同条件とは? 3組の辺がそれぞれ等しい 2組の辺とその間の角がそれぞれ等しい 1組の辺とその両端の角がそれぞれ等しい 合同な三角形を見つける問題に挑戦! 演習問題で理解を深める! 合同な図形の見つけ方 まとめ がんばっているのに60点の壁をクリアできない中3生の方

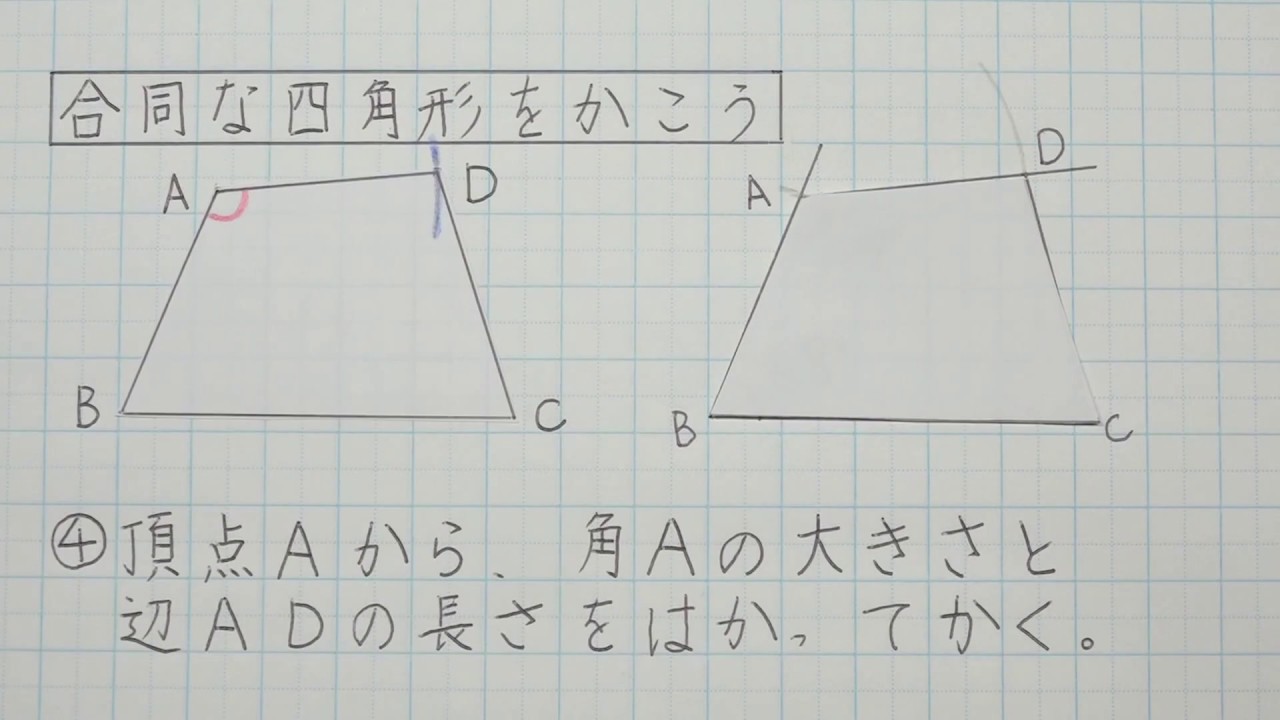
5年算数 図形の角と合同 5 合同な四角形をかこう Youtube
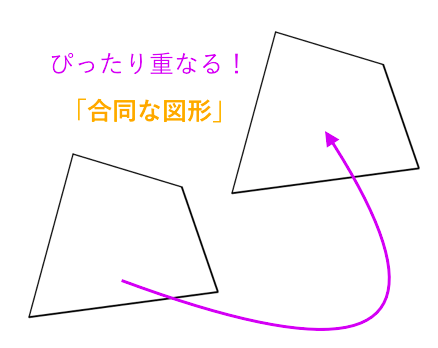
26/6/22 また、辺の数に関係なく、二つの多角形の面積が等しければ、適当に分割することによって、二つの多角形を合同にすることができる。(ボヤイの定理) 相似条件 辺の数が同数の二つの多角形 p , p' があるとする。 三角形の合同 本節では図形の合同について考えてみましょう。平面上の2つの図形について、一方を移動・回転・反転することで他方に重ね合わせることができるとき、この2つの図形は合同であるといいます。そして合同であることを記号 $\equiv$ で表します。24/7/21 続きを読む 和から株式会社|大人のための数学教室 三角形は合同条件によりその形、大きさが一意に定まります。 つまり、合同条件により三角形の面積が決まるはずです。 本記事では合同条件に出てくる辺の長さや角度の大きさからどのように三角形
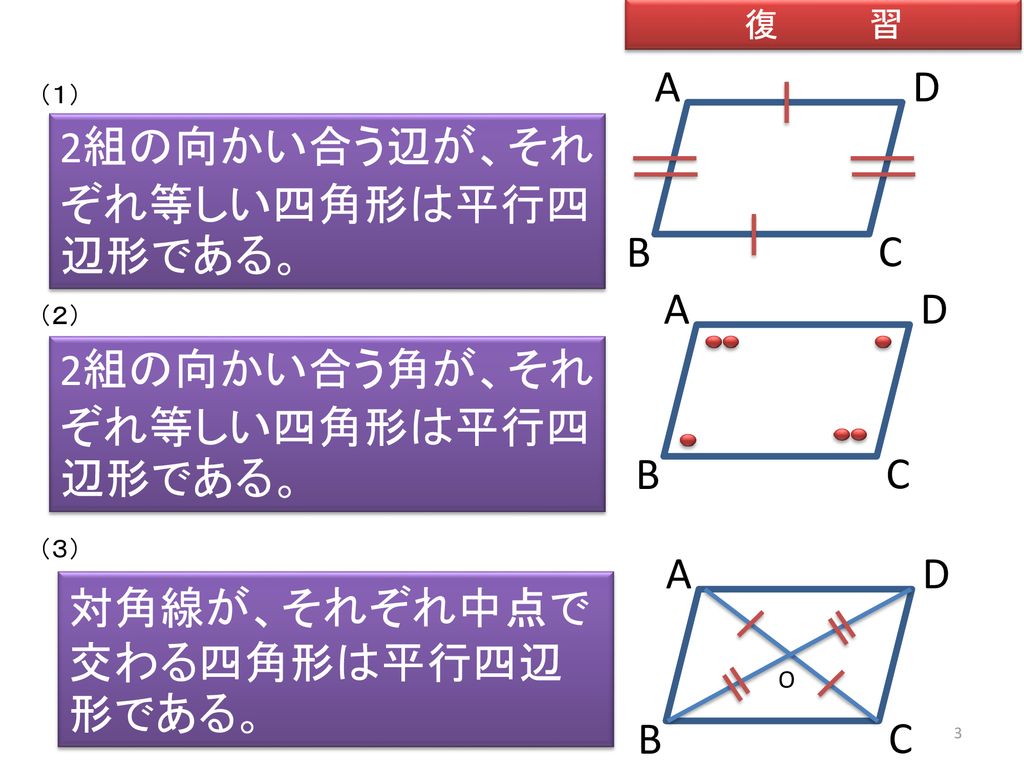
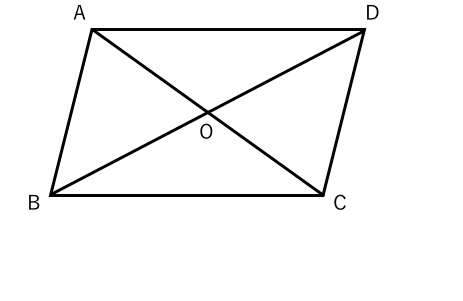
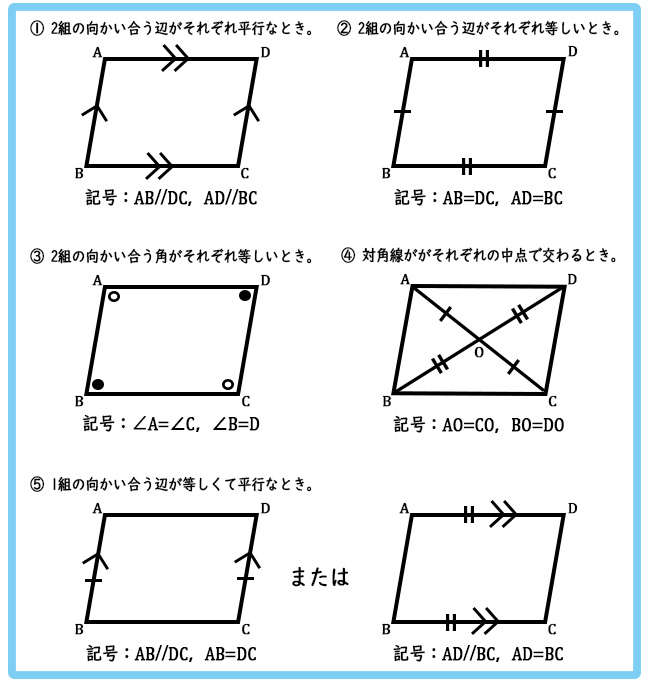
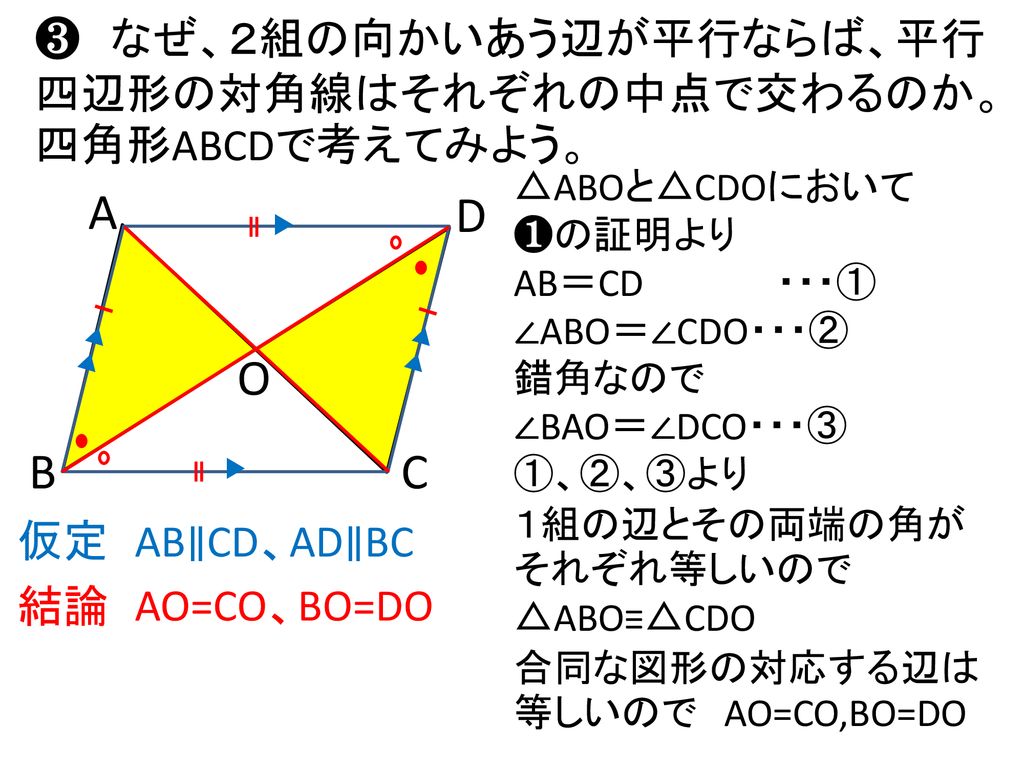
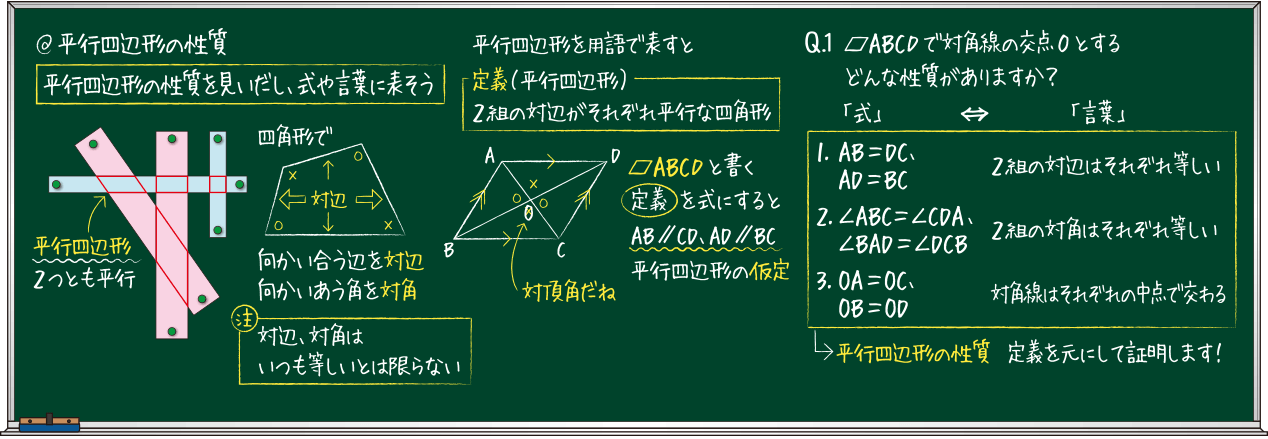
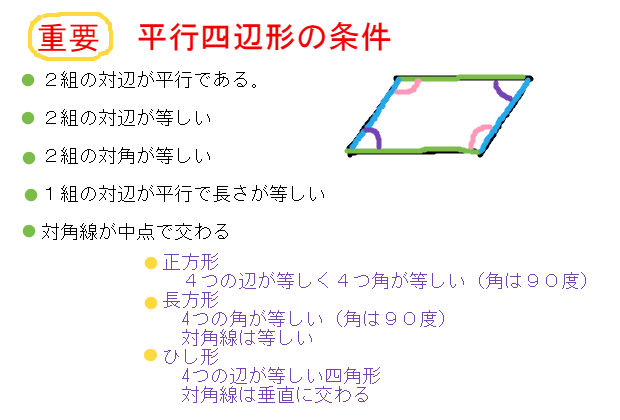
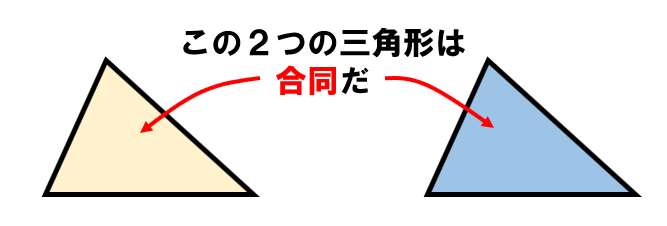
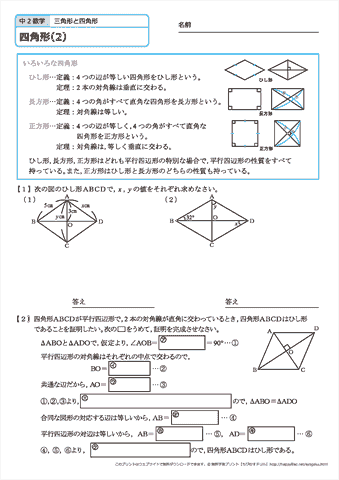
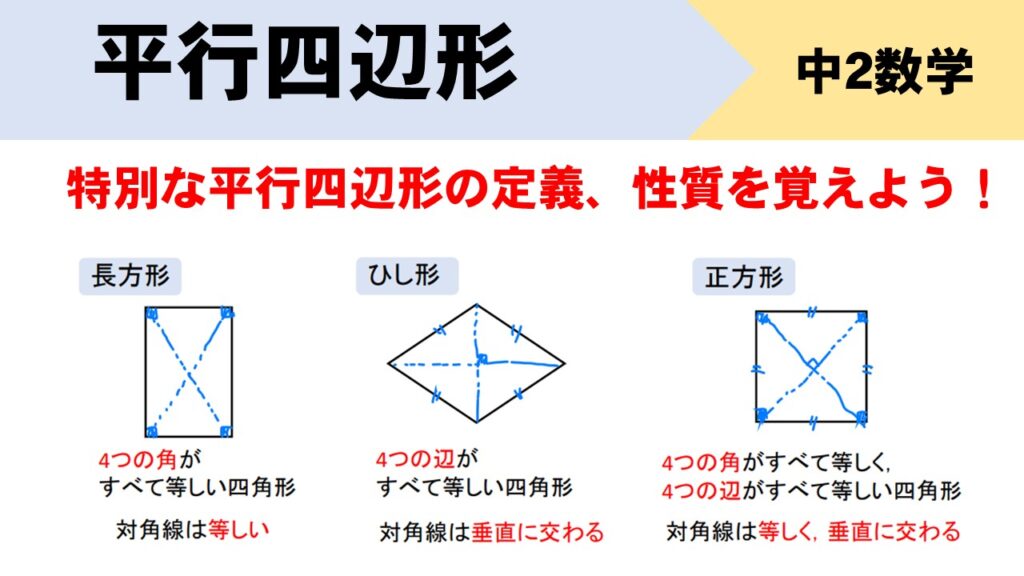
ゆず 🌸 4年以上前 平行四辺形の合同条件 ①2組の対辺はそれぞれ平行である ②2組の対辺はそれぞれ等しい ③2組の対角はそれぞれ等しい ④対角線はそれぞれの中点で交わる ⑤1組の対辺は、平行で長さ29/9/21 問題 問題三角形と四角形・直角三角形の合同条件(中学2年生:第57回) 中学数学講座中2・三角形と四角形動画講座一覧ページ 中学数学講座・動画一覧ページ テストの点・成績アップ・読解力・思考力の習得のカギは「自習力」! どんなに成の視座から四角形の合同条件を,教科専門性を 学ぶ上で相応しい題材であると指摘している.こ れに関連した先行研究として,例えば増島(07) は,四角形の合同条件を三角形分割への帰着か折 れ線による形状決定かに大別した上で,合同条件
四角形 の 合同 条件のギャラリー
各画像をクリックすると、ダウンロードまたは拡大表示できます
 | ||
 |  |  |
 |  | |
「四角形 の 合同 条件」の画像ギャラリー、詳細は各画像をクリックしてください。
 | ||
 |  | |
 |  | |
「四角形 の 合同 条件」の画像ギャラリー、詳細は各画像をクリックしてください。
 |  |  |
 |  |  |
 |  | |
「四角形 の 合同 条件」の画像ギャラリー、詳細は各画像をクリックしてください。
 |  | |
 |  |  |
 |  | |
「四角形 の 合同 条件」の画像ギャラリー、詳細は各画像をクリックしてください。
 | ||
 |  | |
 | ||
「四角形 の 合同 条件」の画像ギャラリー、詳細は各画像をクリックしてください。
 |  |  |
 |  | |
 |  |  |
「四角形 の 合同 条件」の画像ギャラリー、詳細は各画像をクリックしてください。
 |  | |
 | ||
 | ||
「四角形 の 合同 条件」の画像ギャラリー、詳細は各画像をクリックしてください。
 |  |  |
 |  |  |
 |  |  |
「四角形 の 合同 条件」の画像ギャラリー、詳細は各画像をクリックしてください。
 |  |  |
 |  |  |
 |  | |
「四角形 の 合同 条件」の画像ギャラリー、詳細は各画像をクリックしてください。
 |  | |
 |  | |
 |  |  |
「四角形 の 合同 条件」の画像ギャラリー、詳細は各画像をクリックしてください。
 |  | |
 |  | |
 |  |  |
「四角形 の 合同 条件」の画像ギャラリー、詳細は各画像をクリックしてください。
 |  |  |
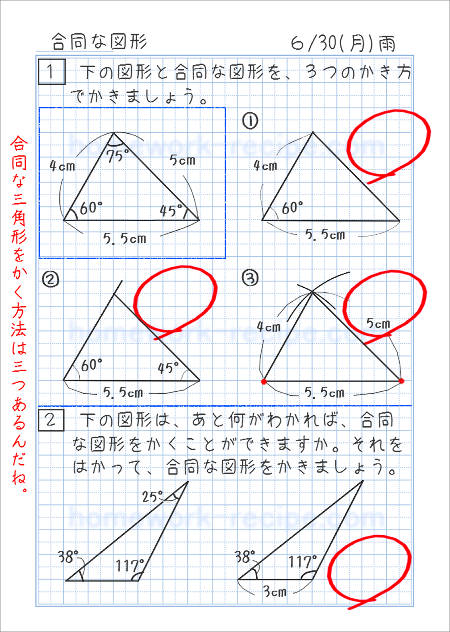
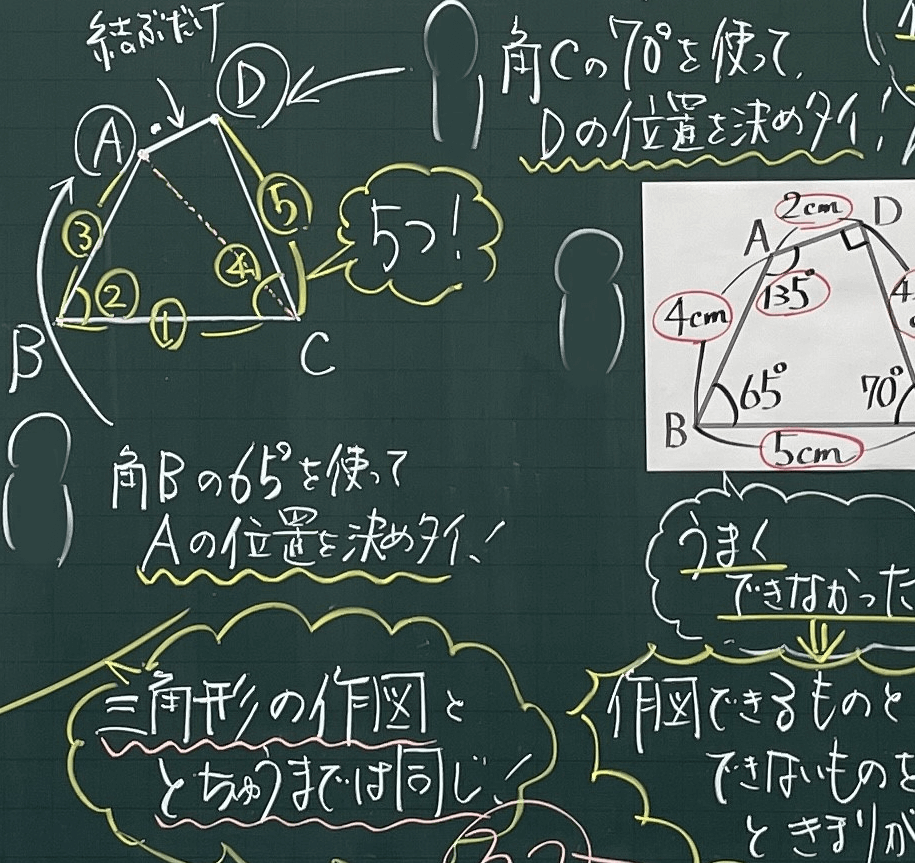
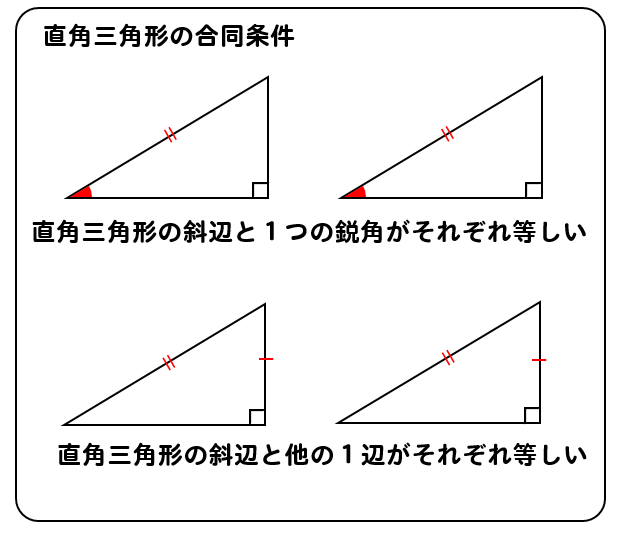
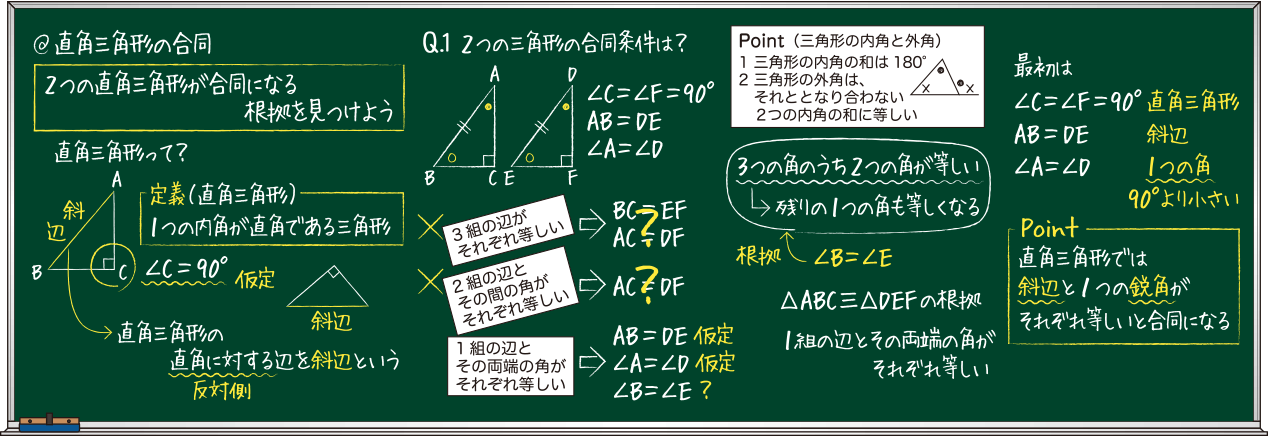
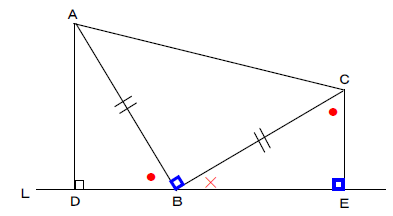
③ 1つの辺とその両はしの角 合同な三角形のかき方 チャレンジシート① 学ぶ 三角形のかき方は三つあるんで すね。それぞれ,わかっているこ とを使ってかくと,三角形がかけ るんですね。 三角形のかき方を使って,四角形もか くことができます。直角三角形の合同条件とは 直角三角形は、以下のことが分かれば合同だと言えます。 今までの三角形の合同条件が このように、3つの情報を組み合わせて合同を言うことができましたが 直角三角形の場合には このように2つの情報だけでOKになります





0 件のコメント:
コメントを投稿